Cho tam giác ABC có trung tuyến AM. Chứng minh rằng \(AM^2=\dfrac{2\left(AB^2+AC^2\right)-BC^2}{4}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
0
19 tháng 9 2023
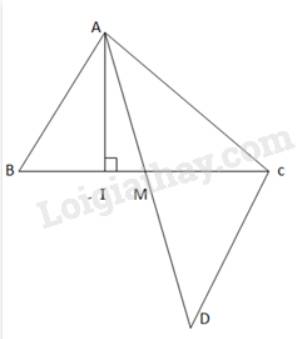
a)
AI là đường vuông góc kẻ từ A xuống đoạn thẳng BC.
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}AI < AB\\AI < AC\end{array} \right.\\ \Rightarrow 2AI < AB + AC\\ \Rightarrow AI < \dfrac{1}{2}\left( {AB + AC} \right)\end{array}\) (đường vuông góc nhỏ hơn đường xiên)
b)
Lấy D sao cho M là trung điểm của AD
Xét \(\Delta ABM\) và \(DCM\) có
AM = DM ( do M là trung điểm của AD)
BM = CM ( do M là trung điểm của BC)
\(\widehat {AMB} = \widehat {CMD}\)( 2 góc đối đỉnh)
\( \Rightarrow \Delta ABM = \Delta DCM\left( {c - g - c} \right)\)
\( \Rightarrow AB = CD\)(2 cạnh tương ứng)
Xét \(\Delta ADC\) ta có: AD < AC + CD (bất đẳng thức tam giác)
\( \Rightarrow \) 2AM < AC + AB
\( \Rightarrow \) AM < \(\dfrac{1}{2}\)(AB + AC)
L
27 tháng 2 2016
Kẻ AH | BC.
Xét \(\Delta AHB\) vuông tại H:
\(AH^2+HB^2=AB^2\) (Định lý Pytago)
\(\Rightarrow AH^2=AB^2-HB^2\)
Xét \(\Delta AHM\) vuông tại H:
\(AH^2+HM^2=AM^2\)(Định lý Pytago)
\(\Rightarrow\left(AB^2-HB^2\right)+HM^2=AM^2\)
\(AB^2+\left(HM-HB\right)\left(HM+HB\right)=AB^2+BM.\left(HM-HB\right)=AB^2+\frac{1}{2}BC\left(HM-HB\right)=AM^2\)
\(\Rightarrow AB^2=AM^2-\frac{1}{2}BC\left(HM-HB\right)\)
Xét \(\Delta AHC\) vuông tại H:
\(AH^2+HC^2=AC^2\)(Định lý Pytago)
\(\Rightarrow AC^2-AM^2=HC^2-HM^2=\left(HC-HM\right)\left(HC+HM\right)=MC\left(HC+HM\right)=\frac{1}{2}BC\left(HC+HM\right)\)
\(\Rightarrow AC^2=AM^2+\frac{1}{2}BC\left(HC+HM\right)\)
\(\Rightarrow AB^2+AC^2=AM^2-\frac{1}{2}BC\left(HM-HB\right)+AM^2+\frac{1}{2}BC\left(HC+HM\right)\)
\(=2AM^2+\frac{1}{2}BC.\left(HC+HM-HM+HB\right)\)
\(=2AM^2+\frac{1}{2}BC^2\)
\(\Rightarrow2\left(AB^2+AC^2\right)=2\left(2AM^2+\frac{1}{2}BC^2\right)\)
\(2AB^2+2AC^2=4AM^2+BC^2\)
\(\Rightarrow2AB^2+2AC^2-BC^2=4AM^2\)
LM
27 tháng 2 2016
áp dụng hệ thức lượng trong tam giác
AM2=(AB2+AC2)/2-BC2/4
2AM2=AB2+AC2-1/2.BC2
2AM2+1/2.BC2=AB2+AC2-1/2BC2+1/2BC2=AB2...
chúc bạn thành công!!!
HB
0
Hình như đề bị thiếu dữ kiện á, bạn xem lại đề ghi đủ chưa nha
Đủ rồi đó bạn.