Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bài 2:
ta có : điểm M nằm trên đường trung trực của BC nên M sẽ cách đều B và C => MB=MC
Ta có: AC=AM+MC
=> AC=AM+MB
Bài 2: Tam giác BNC cân tại N vì đường thẳng hạ từ N xuống vuong góc cạnh đối diện cũng là trung tuyến nên BN=NC
=> AN+BN=AN+NC=AC

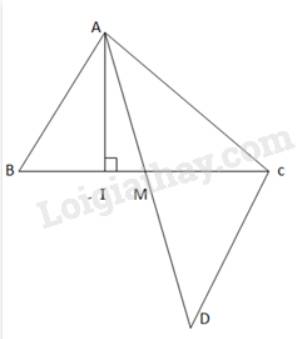
a)
AI là đường vuông góc kẻ từ A xuống đoạn thẳng BC.
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}AI < AB\\AI < AC\end{array} \right.\\ \Rightarrow 2AI < AB + AC\\ \Rightarrow AI < \dfrac{1}{2}\left( {AB + AC} \right)\end{array}\) (đường vuông góc nhỏ hơn đường xiên)
b)
Lấy D sao cho M là trung điểm của AD
Xét \(\Delta ABM\) và \(DCM\) có
AM = DM ( do M là trung điểm của AD)
BM = CM ( do M là trung điểm của BC)
\(\widehat {AMB} = \widehat {CMD}\)( 2 góc đối đỉnh)
\( \Rightarrow \Delta ABM = \Delta DCM\left( {c - g - c} \right)\)
\( \Rightarrow AB = CD\)(2 cạnh tương ứng)
Xét \(\Delta ADC\) ta có: AD < AC + CD (bất đẳng thức tam giác)
\( \Rightarrow \) 2AM < AC + AB
\( \Rightarrow \) AM < \(\dfrac{1}{2}\)(AB + AC)

Xét ΔABC có
BD,CE là trung tuyến
BD cắt CE tại G
=>G là trọng tâm
=>M là trung điểm của BC
Lấy D sao cho M là trung điểm của AD
Xet tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>AD>AC+CD=AC+AB
=>AM<1/2(AB+AC)

Ta có: \(\Delta\)ABC có AB=AC
\(\Rightarrow\)\(\Delta\)ABC cân tại A
\(\Rightarrow\)\(\widehat{KBC}\)\(=\)\(\widehat{HCB}\)
Xét hai \(\Delta\)vuông CKB và BHC có:
BC là cạnh huyền chung (gt)
\(\widehat{KBC}\)\(=\)\(\widehat{HCB}\) (cmt)
\(\Rightarrow\)\(\Delta\)CKB\(=\)\(\Delta\)BHC (ch-gn)
\(\Rightarrow\)BH=CK(hai cạnh tương ứng)
\(\Rightarrow\)dpcm
Giải
Ta có hình vẽ:
Xét 2 \(\Delta BHA\) và \(\Delta CKA\). Có:
góc A chung
Góc H1 = K1
AB=AC
\(\Rightarrow\) \(\Delta BHA=\Delta CKA\) (g.c.g)
\(\Rightarrow\) BH = CK ( 2 cạnh tương ứng )
\(\Rightarrow\) đpcm