Giúp mình bài 3 với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2.
\(cosx+cos3x=1+\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow2cos2x.cosx=1+cos2x+sin2x\)
\(\Leftrightarrow2cos2x.cosx=2cos^2x+2sinx.cosx\)
\(\Leftrightarrow cosx\left(cos2x-cosx-sinx\right)=0\)
\(\Leftrightarrow cosx\left(cos^2x-sin^2x-cosx-sinx\right)=0\)
\(\Leftrightarrow cosx\left(cosx+sinx\right)\left(cosx-sinx-1\right)=0\)
\(\Leftrightarrow cosx.\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right).\left[\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)-1\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sin\left(x+\dfrac{\pi}{4}\right)=0\\cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=-\dfrac{\pi}{4}+k\pi\\x+\dfrac{\pi}{4}=\pm\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=-\dfrac{\pi}{4}+k\pi\\x=k2\pi\end{matrix}\right.\)

2b)
Áp dụng BĐT bunhiacopxki có:
\(\left(1+1\right)\left(x^4+y^4\right)\ge\left(x^2+y^2\right)^2\)
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x+y\right)^2\)\(\Leftrightarrow x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)
\(\Rightarrow2\left(x^4+y^4\right)\ge\dfrac{\left(x+y\right)^4}{4}\Leftrightarrow x^4+y^4\ge\dfrac{1}{8}.\left(x+y\right)^4\)
Dấu "=" xảy ra khi x=y
3)
Áp dụng bđt Holder có:
\(\left(x^3+y^3+z^3\right)\left(1+1+1\right)\left(1+1+1\right)\ge\left(x+y+z\right)^3\)
\(\Leftrightarrow x^3+y^3+z^3\ge\dfrac{1}{9}\left(x+y+z\right)^3\)
Dấu "=" xảy ra khi x=y=z
3)(Nếu không dùng Holder)
Với x,y,z >0, ta có bđt sau:\(2x^3+2y^3+2z^3\ge xy\left(x+y\right)+yz\left(y+z\right)+xz\left(x+z\right)\) (1)
Thật vậy (1)\(\Leftrightarrow\left(x+y\right)\left(x^2-xy+y^2\right)-xy\left(x+y\right)+\left(y+z\right)\left(y^2-yz+z^2\right)-yz\left(y+z\right)+\left(z+x\right)\left(z^2-zx+x^2\right)-zx\left(x+z\right)\ge0\)
\(\Leftrightarrow\left(x+y\right)\left(x-y\right)^2+\left(y+z\right)\left(y-z\right)^2+\left(z+x\right)\left(z-x\right)^2\ge0\) (lđ)
Áp dụng AM-GM có:
\(x^3+y^3+z^3\ge3xyz\)
\(\Leftrightarrow\dfrac{2\left(x^3+y^3+z^3\right)}{3}\ge2xyz\) (2)
Từ (1) và (2), cộng vế với vế \(\Rightarrow\dfrac{8}{3}\left(x^3+y^3+z^3\right)\ge xy\left(x+y\right)+yz\left(x+z\right)+xz\left(x+z\right)+2xyz\)
\(\Leftrightarrow\dfrac{8}{3}\left(x^3+y^3+z^3\right)\ge\left(x+y\right)\left(y+z\right)\left(z+x\right)\)
\(\Leftrightarrow8\left(x^3+y^3+z^3\right)\ge3\left(x+y\right)\left(y+z\right)\left(x+z\right)\)
\(\Leftrightarrow9\left(x^3+y^3+z^3\right)\ge x^3+y^3+z^3+3\left(x+y\right)\left(y+z\right)\left(z+x\right)=\left(x+y+z\right)^3\)
\(\Rightarrow x^3+y^3+z^3\ge\dfrac{1}{9}\left(x+y+z\right)^3\) (đpcm)

\(3,\\ a,ĐK:x\ge-5\\ PT\Leftrightarrow2\sqrt{x+5}-2\sqrt{x+5}+3\sqrt{x+5}=12\\ \Leftrightarrow\sqrt{x+5}=4\Leftrightarrow x+5=16\Leftrightarrow x=11\left(tm\right)\\ b,ĐK:x\in R\\ PT\Leftrightarrow\left|x-5\right|=6\Leftrightarrow\left[{}\begin{matrix}x-5=6\\5-x=6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=11\\x=-1\end{matrix}\right.\)

e thay dấu = cho tất cả phsố trog bài 3 rồi tìm x , khi tìm x thì coi dấu của bài r nói x lớn hoặc nhỏ hơn số đó là đc

\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)

3:
c: Xét ΔCAM có KI//AM
nên KI/AM=CI/CM
Xét ΔCMB có HI//MB
nên HI/MB=CI/CM
=>KI/AM=HI/MB
=>KI=HI
=>I là trung điểm của HK

III
1 It's colder today than yesterday
2 It takes 4 hours to travel by car and fives hours by train
3 We were busier at work today than everyday
4 Jane's sister cooks worse than her
5 Nobody in this team can play football as well as Tom
IV
1 D
2 A

Gọi x,y,z là số học sinh khối 6, 7, 8
(x,y,z>0, đvị là học sinh)
Đã biết khối học sinh lớp 8 ít hơn số hs khối 6 là 120 hs
x-z=120
x, y, z tỉ lệ với 8, 7, 5
x/8=y/7=z/5
Áp dụng tính chất dãy tỉ số bằng nhau có:
x/8=y/7=z/5= x-z/8-5=120/3=40
=> x/8= 40 => x=40.8=320 => số hs khối 6 là 320 hs
y/7= 40 y=40.7= 280 số hs khối 7 là 280 hs
z/5= 40 z=40.5=200 số hs khối 8 là 200 hs



 Giúp mình bài 2b với bài 3 với ạ
Giúp mình bài 2b với bài 3 với ạ

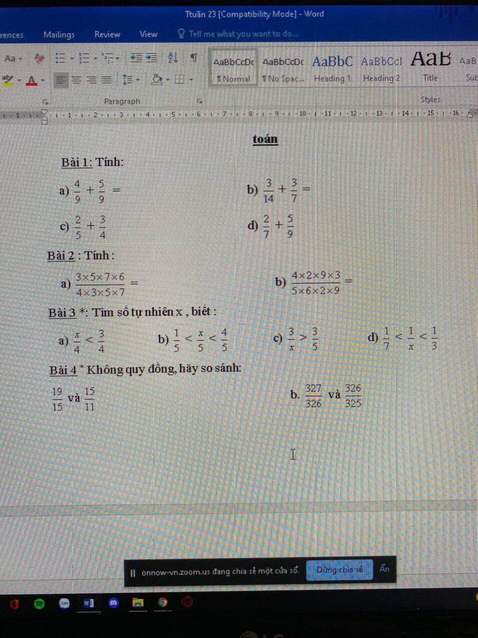


 giúp mình với ạ,mình xin cảm ơn trước
giúp mình với ạ,mình xin cảm ơn trước
Bài 3:
\(n_{Fe}=\dfrac{16,8}{56}=0,3\left(mol\right)\\ a,PTHH:3Fe+2O_2\rightarrow\left(t^o\right)Fe_3O_4\\ b,n_{Fe_3O_4}=\dfrac{0,3}{3}=0,1\left(mol\right)\\ \Rightarrow m_{Fe_3O_4}=232.0,1=23,2\left(g\right)\\ c,n_{O_2}=\dfrac{2}{3}.0,3=0,2\left(mol\right)\\ V_{O_2\left(đktc\right)}=0,2.22,4=4,48\left(l\right)\\ V_{kk\left(đktc\right)}=4,48.5=22,4\left(l\right)\)
Câu 4:
\(n_P=\dfrac{m_p}{M_p}=\dfrac{1,24}{31}=0,04mol\)
\(4P+5O_2\rightarrow\left(t^o\right)2P_2O_5\)
4 5 2 ( mol )
0,04 0,05 0,02 ( mol )
\(m_{P_2O_5}=n_{P_2O_5}.M_{P_2O_5}=0,02.142=2,84g\)
\(V_{O_2}=n_{O_2}.22,4=0,05.22,4=1,12l\)
\(V_{kk}=\dfrac{V_{O_2}}{\dfrac{1}{5}}=\dfrac{1,12}{\dfrac{1}{5}}=5,6l\)