
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(3,\\ a,ĐK:x\ge-5\\ PT\Leftrightarrow2\sqrt{x+5}-2\sqrt{x+5}+3\sqrt{x+5}=12\\ \Leftrightarrow\sqrt{x+5}=4\Leftrightarrow x+5=16\Leftrightarrow x=11\left(tm\right)\\ b,ĐK:x\in R\\ PT\Leftrightarrow\left|x-5\right|=6\Leftrightarrow\left[{}\begin{matrix}x-5=6\\5-x=6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=11\\x=-1\end{matrix}\right.\)



toán 9 mà sao câu 2a có giai thừa vậy bạn ??
chờ mình xíu nhé


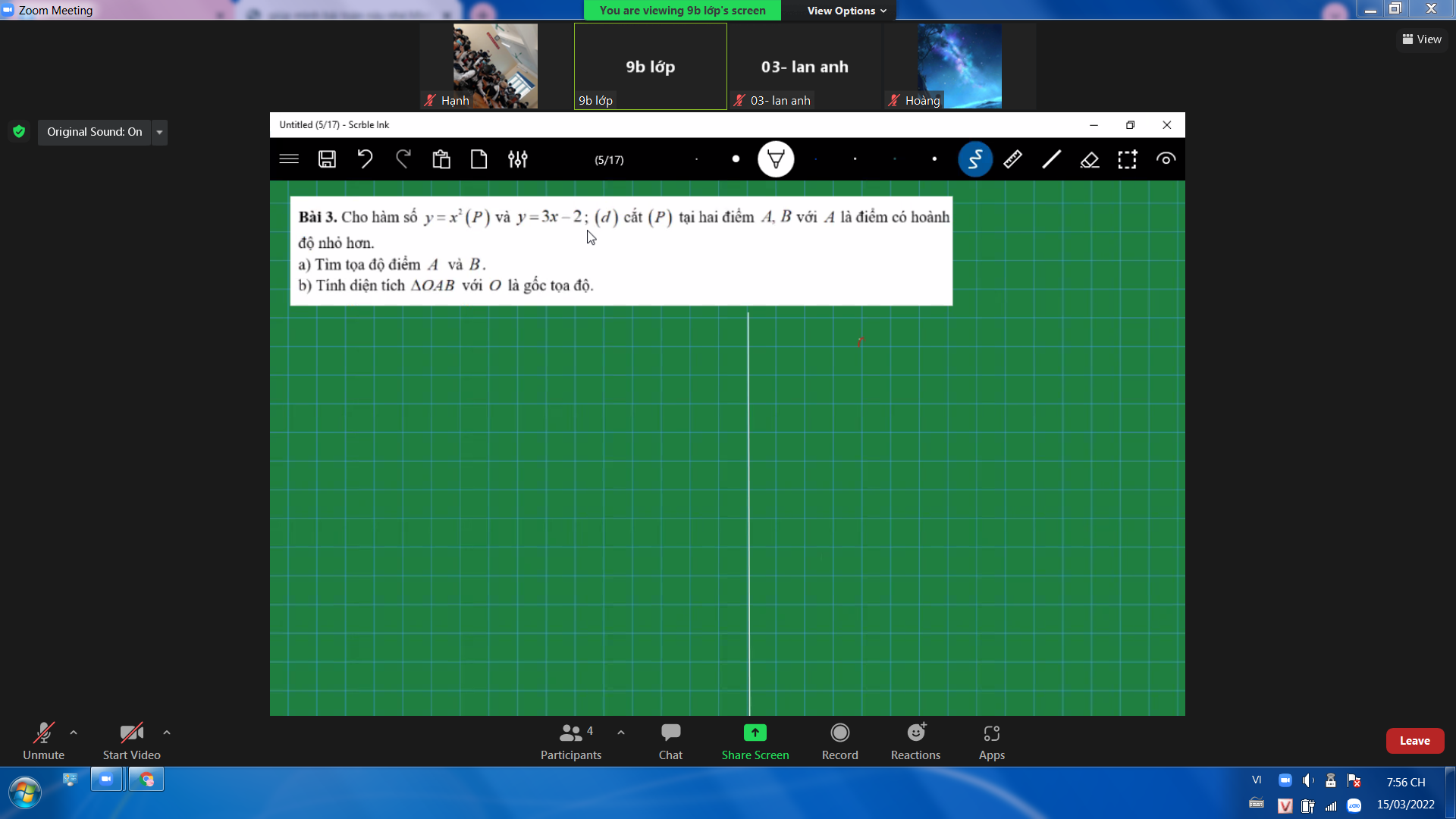
Bài 3:
b: Phương trình hoành độ giao điểm là: \(\dfrac{1}{2}x^2-\left(m-1\right)x+\dfrac{1}{2}=0\)
\(\Leftrightarrow x^2-x\left(2m-2\right)+1=0\)
\(\text{Δ}=\left(2m-2\right)^2-4=\left(2m-6\right)\left(2m+2\right)\)
Để (P) cắt (d) tại hai điểm phân biệt thì(m-3)(m+1)>0
=>m>3 hoặc m<-1

3.1
\(\frac{3+\sqrt{3}}{1+\sqrt{3}}=\frac{\sqrt{3}(\sqrt{3}+1)}{\sqrt{3}+1}=\sqrt{3}\)
3.2
\(=\frac{4(\sqrt{5}-1)-4(\sqrt{5}+1)}{(\sqrt{5}-1)(\sqrt{5}+1)}:\sqrt{(\sqrt{2}+1)^2}\)
\(=\frac{-8}{4}:(\sqrt{2}+1)=\frac{-2}{\sqrt{2}+1}=\frac{-2(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}=\frac{-2(\sqrt{2}-1)}{1}=2(1-\sqrt{2})\)
3.3.
\(=\frac{\sqrt{2}+1-(\sqrt{2}-1)}{(\sqrt{2}-1)(\sqrt{2}+1)}:\sqrt{(\sqrt{2}-1)^2}=\frac{2}{1}:(\sqrt{2}-1)=\frac{2}{\sqrt{2}-1}=\frac{2(\sqrt{2}+1)}{(\sqrt{2}-1)(\sqrt{2}+1)}=2(\sqrt{2}+1)\)
3.4 Cái này đã gọn lắm rồi không cần rút gọn nữa.
3.5
\(=\frac{(\sqrt{5}+\sqrt{3})^2+(\sqrt{5}-\sqrt{3})^2}{(\sqrt{5}-\sqrt{3})(\sqrt{5}+\sqrt{3})}=\frac{16}{5-3}=8\)
3.6
\(=\frac{(\sqrt{5}-1)^2-(\sqrt{5}+1)^2}{(\sqrt{5}+1)(\sqrt{5}-1)}=\frac{-4\sqrt{5}}{5-1}=-\sqrt{5}\)

 Giúp mình bài 2b với bài 3 với ạ
Giúp mình bài 2b với bài 3 với ạ




 giúp mình bài 3 với ạ
giúp mình bài 3 với ạ

2b)
Áp dụng BĐT bunhiacopxki có:
\(\left(1+1\right)\left(x^4+y^4\right)\ge\left(x^2+y^2\right)^2\)
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x+y\right)^2\)\(\Leftrightarrow x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)
\(\Rightarrow2\left(x^4+y^4\right)\ge\dfrac{\left(x+y\right)^4}{4}\Leftrightarrow x^4+y^4\ge\dfrac{1}{8}.\left(x+y\right)^4\)
Dấu "=" xảy ra khi x=y
3)
Áp dụng bđt Holder có:
\(\left(x^3+y^3+z^3\right)\left(1+1+1\right)\left(1+1+1\right)\ge\left(x+y+z\right)^3\)
\(\Leftrightarrow x^3+y^3+z^3\ge\dfrac{1}{9}\left(x+y+z\right)^3\)
Dấu "=" xảy ra khi x=y=z
3)(Nếu không dùng Holder)
Với x,y,z >0, ta có bđt sau:\(2x^3+2y^3+2z^3\ge xy\left(x+y\right)+yz\left(y+z\right)+xz\left(x+z\right)\) (1)
Thật vậy (1)\(\Leftrightarrow\left(x+y\right)\left(x^2-xy+y^2\right)-xy\left(x+y\right)+\left(y+z\right)\left(y^2-yz+z^2\right)-yz\left(y+z\right)+\left(z+x\right)\left(z^2-zx+x^2\right)-zx\left(x+z\right)\ge0\)
\(\Leftrightarrow\left(x+y\right)\left(x-y\right)^2+\left(y+z\right)\left(y-z\right)^2+\left(z+x\right)\left(z-x\right)^2\ge0\) (lđ)
Áp dụng AM-GM có:
\(x^3+y^3+z^3\ge3xyz\)
\(\Leftrightarrow\dfrac{2\left(x^3+y^3+z^3\right)}{3}\ge2xyz\) (2)
Từ (1) và (2), cộng vế với vế \(\Rightarrow\dfrac{8}{3}\left(x^3+y^3+z^3\right)\ge xy\left(x+y\right)+yz\left(x+z\right)+xz\left(x+z\right)+2xyz\)
\(\Leftrightarrow\dfrac{8}{3}\left(x^3+y^3+z^3\right)\ge\left(x+y\right)\left(y+z\right)\left(z+x\right)\)
\(\Leftrightarrow8\left(x^3+y^3+z^3\right)\ge3\left(x+y\right)\left(y+z\right)\left(x+z\right)\)
\(\Leftrightarrow9\left(x^3+y^3+z^3\right)\ge x^3+y^3+z^3+3\left(x+y\right)\left(y+z\right)\left(z+x\right)=\left(x+y+z\right)^3\)
\(\Rightarrow x^3+y^3+z^3\ge\dfrac{1}{9}\left(x+y+z\right)^3\) (đpcm)