Giúp em 2 đề này với ạ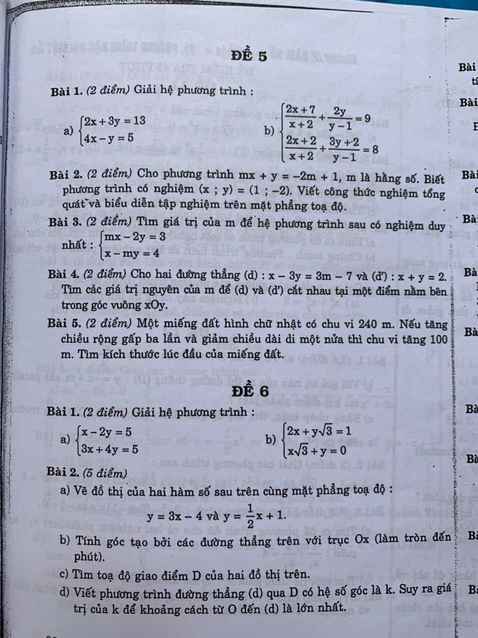
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
2
DT
Đỗ Thanh Hải
CTVVIP
25 tháng 5 2021
Đề dài thế này sao giải thích nhanh cho e đc
Part 1
1 C
2 B
3 D
4 C
5 B
6 A
Part 2
1 T
2 F
3 F
4 F
V
1 That old house has just been bought
2 If he doesn't take these pills, he won't be better
3 I suggest taking a train
4 Spending the weekend in the countryside is very wonderful
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
1.a
\(\lim\limits_{x\rightarrow2}\dfrac{x^3+3x^2-9x-2}{x^3-x-6}=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x^2+5x+1\right)}{\left(x-2\right)\left(x^2+2x+3\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{x^2+5x+1}{x^2+2x+3}=\dfrac{15}{11}\)
b.
\(\lim\limits_{x\rightarrow-\infty}\left(\sqrt{x^2-x+3}+x\right)=\lim\limits_{x\rightarrow-\infty}\dfrac{-x+3}{\sqrt{x^2-x+3}-x}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{-1+\dfrac{3}{x}}{-\sqrt{1-\dfrac{1}{x}+\dfrac{3}{x^2}}-1}=\dfrac{-1}{-2}=\dfrac{1}{2}\)
H9
HT.Phong (9A5)
CTVHS
15 tháng 12 2023
Câu II:
a) \(\sqrt{2x-1}=\sqrt{5}\left(x\ge\dfrac{1}{2}\right)\)
\(\Leftrightarrow2x-1=5\)
\(\Leftrightarrow2x=5+1\)
\(\Leftrightarrow2x=6\)
\(\Leftrightarrow x=\dfrac{6}{2}\)
\(\Leftrightarrow x=3\left(tm\right)\)
b) \(6\sqrt{x-5}+\sqrt{9x-45}-2\sqrt{4x-20}=25\left(x\ge5\right)\)
\(\Leftrightarrow6\sqrt{x-5}+\sqrt{9\left(x-5\right)}-2\sqrt{4\left(x-5\right)}=25\)
\(\Leftrightarrow6\sqrt{x-5}+3\sqrt{x-5}-2\cdot2\sqrt{x-5}=25\)
\(\Leftrightarrow9\sqrt{x-5}-4\sqrt{x-5}=25\)
\(\Leftrightarrow5\sqrt{x-5}=25\)
\(\Leftrightarrow\sqrt{x-5}=5\)
\(\Leftrightarrow x-5=5^2\)
\(\Leftrightarrow x-5=25\)
\(\Leftrightarrow x=30\left(tm\right)\)
15 tháng 12 2023
Bài III:
a:
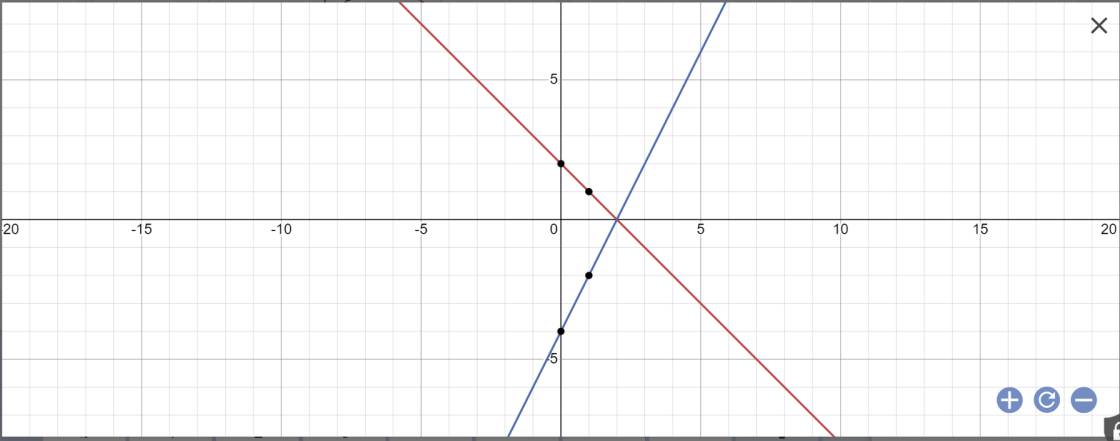
b: phương trình hoành độ giao điểm là:
2x-4=-x+2
=>2x+x=4+2
=>3x=6
=>x=6/3=2
Thay x=2 vào y=-x+2, ta được:
\(y=-2+2=0\)
Vậy: A(2;0)
c: Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=-x+2=-0+2=2\end{matrix}\right.\)
Vậy: B(0;2)
Tọa độ C là:
\(\left\{{}\begin{matrix}x=0\\y=2x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\cdot0-4=-4\end{matrix}\right.\)
Vậy: C(0;-4)
Ta có: A(2;0); B(0;2); C(0;-4)
\(AB=\sqrt{\left(0-2\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)
\(AC=\sqrt{\left(0-2\right)^2+\left(-4-0\right)^2}=\sqrt{4^2+2^2}=2\sqrt{5}\)
\(BC=\sqrt{\left(0-0\right)^2+\left(-4-2\right)^2}=6\)
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{8+20-36}{2\cdot2\sqrt{2}\cdot2\sqrt{5}}=\dfrac{-8}{8\sqrt{5}}=-\dfrac{1}{\sqrt{5}}\)
=>\(sinBAC=\sqrt{1-cos^2BAC}=\sqrt{1-\dfrac{1}{5}}=\dfrac{2}{\sqrt{5}}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)
\(=\dfrac{1}{2}\cdot\dfrac{2}{\sqrt{5}}\cdot2\sqrt{2}\cdot2\sqrt{5}=4\sqrt{2}\)
HK
1
12 tháng 12 2021
Đề 1:
Bài 1:
\(a,=\sqrt{\left(\sqrt{7}+1\right)^2}-\left|-1+\sqrt{7}\right|=\sqrt{7}+1-\sqrt{7}+1=2\\ b,=2\sqrt{2}-4\sqrt{2}-5\sqrt{2}+\dfrac{\sqrt{2}}{2}=\dfrac{\sqrt{2}}{2}-7\sqrt{2}=\dfrac{-13\sqrt{2}}{\sqrt{2}}\)
Bài 2:
\(PT\Leftrightarrow\sqrt{\left(x-\dfrac{1}{2}\right)^2}=\dfrac{1}{2}\Leftrightarrow\left|x-\dfrac{1}{2}\right|=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}+\dfrac{1}{2}=1\\x=-\dfrac{1}{2}+\dfrac{1}{2}=0\end{matrix}\right.\)
Bài 3:
\(a,M=\dfrac{a-2\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{2\sqrt{a}}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}=\dfrac{2\left(\sqrt{a}-1\right)^2}{\left(\sqrt{a}-1\right)^2\left(\sqrt{a}+1\right)}=\dfrac{2}{\sqrt{a}+1}\\ b,M< 1\Leftrightarrow\dfrac{2}{\sqrt{a}+1}-1< 0\Leftrightarrow\dfrac{1-\sqrt{a}}{\sqrt{a}+1}< 0\\ \Leftrightarrow1-\sqrt{a}< 0\left(\sqrt{a}+1>0\right)\\ \Leftrightarrow a>1\)
AH
Akai Haruma
Giáo viên
28 tháng 5 2021
Bài 1:
a)
\(A=\left(\frac{4\sqrt{x}}{\sqrt{x}+2}-\frac{8x}{(\sqrt{x}-2)(\sqrt{x}+2)}\right):\left(\frac{\sqrt{x}-1}{\sqrt{x}(\sqrt{x}-2)}-\frac{2(\sqrt{x}-2)}{\sqrt{x}(\sqrt{x}-2)}\right)\)
\(=\frac{4\sqrt{x}(\sqrt{x}-2)-8x}{(\sqrt{x}-2)(\sqrt{x}+2)}:\frac{\sqrt{x}-1-2(\sqrt{x}-2)}{\sqrt{x}(\sqrt{x}-2)}=\frac{-4x-8\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{\sqrt{x}(\sqrt{x}-2)}{-\sqrt{x}+3}\)
\(=\frac{-4\sqrt{x}(\sqrt{x}+2)}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{\sqrt{x}(\sqrt{x}-2)}{3-\sqrt{x}}=\frac{-4x(\sqrt{x}-2)}{(\sqrt{x}-2)(3-\sqrt{x})}=\frac{4x}{\sqrt{x}-3}\)
b)
Ta có:
\(m(\sqrt{x}-3).A>x+2025\)
\(\Leftrightarrow 4xm>x+2025\Leftrightarrow x(4m-1)>2025\)
\(\Leftrightarrow 4m-1>\frac{2025}{x}\Leftrightarrow m>\frac{1}{4}(\frac{2025}{x}+1)\) với mọi $x>9$
\(\Leftrightarrow m> \max \frac{1}{4}(\frac{2025}{x}+1), \forall x>9\Leftrightarrow m>56,5\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
14 tháng 12 2022
\(m_{H_2O}=1,62\left(g\right)\Rightarrow n_{H_2O}=0,09\left(mol\right)\Rightarrow n_H=0,18\left(mol\right);m_H=0,18.1=0,18\left(g\right)\\ n_{CO_2}=\dfrac{2,64}{44}=0,06\left(mol\right)\Rightarrow n_C=n_{CO_2}=0,06\left(mol\right);m_C=0,06.12=0,72\left(g\right)\\ Vây:m_C+m_H=0,72+0,18=0,9< 1,38\\ \Rightarrow X.có.chứa.O\\ m_O=1,38-0,9=0,48\left(g\right);n_O=\dfrac{0,48}{16}=0,03\left(mol\right)\\ Đặt.X:C_aH_bO_c\left(a,b,c:nguyên,dương\right)\\ Ta.có:a:b:c=0,06:0,18:0,03=2:6:1\\ \Rightarrow CTĐG:C_2H_6O\\ M_X=23.2=46\left(\dfrac{g}{mol}\right)=M_{C_2H_6O}\\ \Rightarrow X:C_2H_6O\)
Bài 1:
a: \(\Leftrightarrow\left\{{}\begin{matrix}2x-4y=10\\3x+4y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-1\end{matrix}\right.\)
b: \(\Leftrightarrow\left\{{}\begin{matrix}2\sqrt{3}x+3y=\sqrt{3}\\2\sqrt{3}x+2y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\sqrt{3}\\x=1\end{matrix}\right.\)