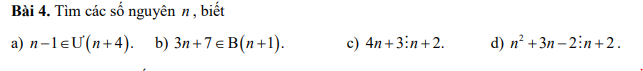
Các bạn trình bày đầy đủ thì mình like nhé:) Nhanh lẹ hộ mik với để mik còn làm btvn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TL
1
3 tháng 1 2022
a: =100x54-100x(-6)
=100x60
=6000
b: =99(123-56+66-123)=990
c: =547x(1+103-4)=54700
d: =-76x10=-760
TL
2
29 tháng 1 2022
Bài 9:
\(a,\left(2n+1\right)⋮\left(n-1\right)\\
\Rightarrow\left[\left(2n-2\right)+3\right]⋮\left(n-1\right)\\
\Rightarrow\left[2\left(n-1\right)+3\right]⋮\left(n-1\right)\)
Mà \(2\left(n-1\right)⋮\left(n-1\right)\Rightarrow3⋮\left(n-1\right)\Rightarrow n-1\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
Ta có bảng:
| n-1 | -3 | -1 | 1 | 3 |
| n | -2(loại) | 0(tm) | 2(tm) | 4(tm) |
Vậy \(n\in\left\{0;2;4\right\}\)
b, c, d bạn làm tương tự nhé
29 tháng 1 2022
Bài 10:
a: Gọi a=UCLN(n+1;2n+3)
\(\Leftrightarrow2n+3-2\left(n+1\right)⋮a\)
\(\Leftrightarrow1⋮a\)
=>a=1
Vậy: n+1/2n+3 là phân số tối giản
b: Gọi a=UCLN(3n+2;5n+3)
\(\Leftrightarrow5\left(3n+2\right)-3\left(5n+3\right)⋮a\)
\(\Leftrightarrow1⋮a\)
=>a=1
Vậy: 3n+2/5n+3 là phân số tối giản
TL
1
2 tháng 1 2022
Bài 4:
a: \(\Leftrightarrow n-1\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{2;0;6;-4\right\}\)
TL
1
10 tháng 1 2022
a: \(-\dfrac{6}{13}=-\dfrac{12}{26}=\dfrac{-18}{39}=-\dfrac{24}{52}=\dfrac{-30}{65}=\dfrac{-36}{78}=\dfrac{-42}{91}\)
b: \(\dfrac{15}{-7}=\dfrac{-15}{7}=\dfrac{-30}{14}=\dfrac{-45}{21}=\dfrac{-60}{28}=\dfrac{-75}{35}=-\dfrac{90}{42}\)
TL
1
TL
1
10 tháng 1 2022
e: Để 4n+1/3n-1 là số nguyên thì \(12n+3⋮3n-1\)
\(\Leftrightarrow3n-1\in\left\{1;-1;7;-7\right\}\)
hay \(n\in\left\{0;-2\right\}\)
4 tháng 1 2022
b: \(\Leftrightarrow n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{0;-2;1;-3;3;-5\right\}\)
c: \(\Leftrightarrow n+2\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{-1;-3;3;-7\right\}\)
d: \(\Leftrightarrow n+2\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{-1;-3;0;-4;2;-6\right\}\)
a: \(\Leftrightarrow n-1\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{2;0;6;-4\right\}\)
10 tháng 1 2022
Bài 4:
a) Áp dụng t/c dtsbn:
\(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{x+y}{4+3}=\dfrac{14}{7}=2\Rightarrow\left\{{}\begin{matrix}x=2.4=8\\y=2.3=6\end{matrix}\right.\)
Vậy....
b) Áp dụng t/c dtsbn:
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{2x}{16}=\dfrac{3y}{36}=\dfrac{2x+3y}{16+36}=\dfrac{13}{52}=\dfrac{1}{4}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{4}.8=2\\y=\dfrac{1}{4}.12=3\end{matrix}\right.\)(nhận)
Vậy...
c: ⇔n+2∈{1;−1;5;−5}⇔n+2∈{1;−1;5;−5}
hay n∈{−1;−3;3;−7}n∈{−1;−3;3;−7}
d: ⇔n+2∈{1;−1;2;−2;4;−4}⇔n+2∈{1;−1;2;−2;4;−4}
hay n∈{−1;−3;0;−4;2;−6}n∈{−1;−3;0;−4;2;−6}
a: ⇔n−1∈{1;−1;5;−5}⇔n−1∈{1;−1;5;−5}
hay n∈{2;0;6;−4}
b: \(\Leftrightarrow n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{0;-2;1;-3;3;-5\right\}\)
c: \(\Leftrightarrow n+2\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{-1;-3;3;-7\right\}\)
d: \(\Leftrightarrow n+2\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{-1;-3;0;-4;2;-6\right\}\)
a: \(\Leftrightarrow n-1\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{2;0;6;-4\right\}\)