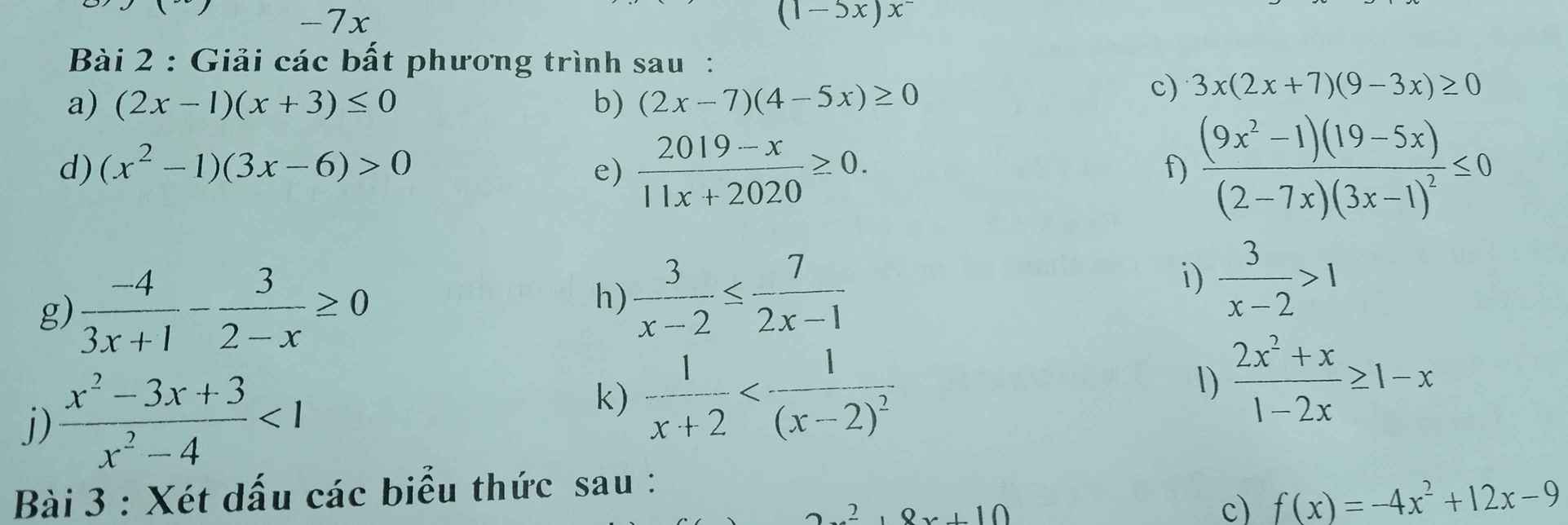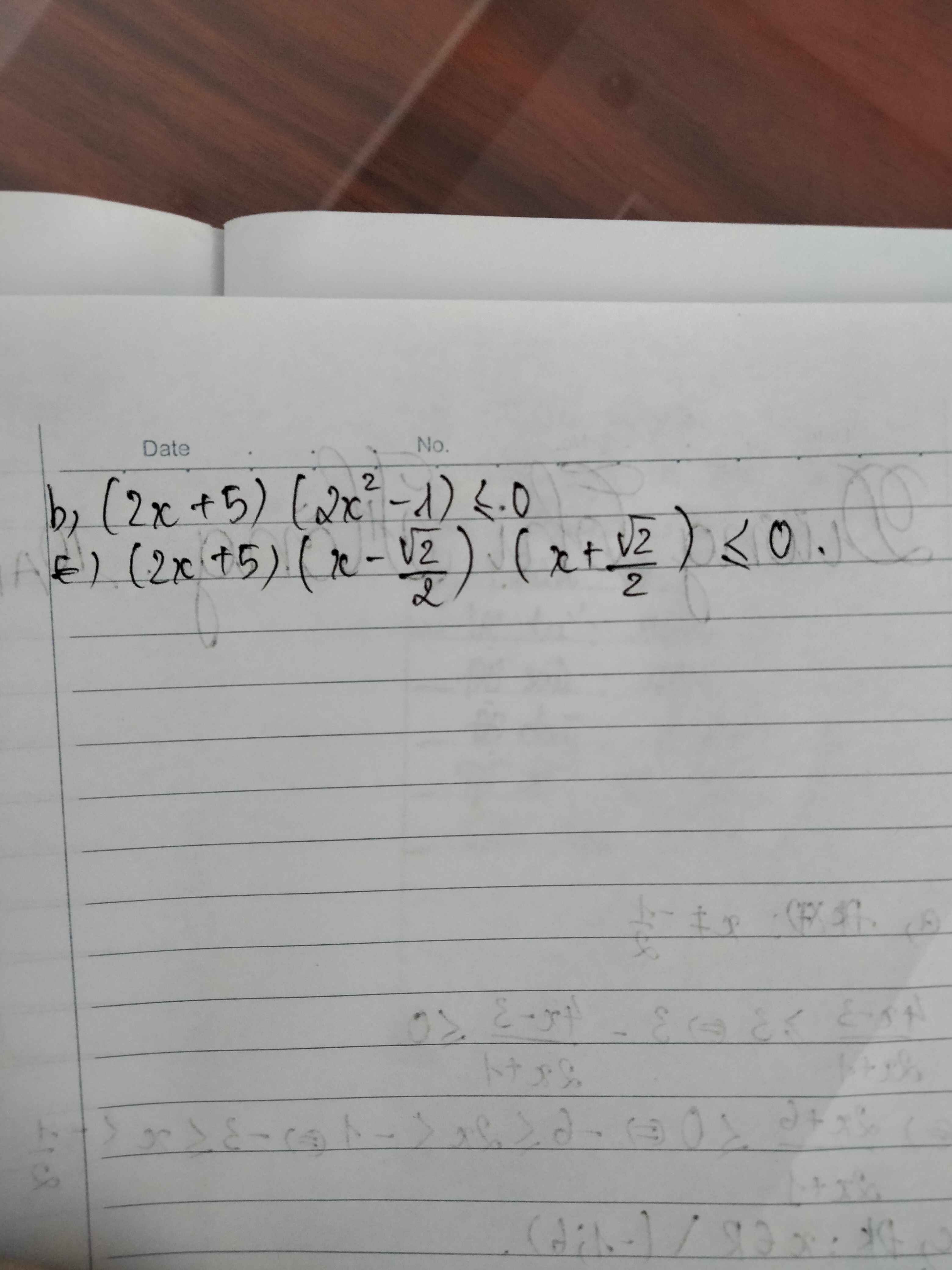Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: (2x-1)(x+3)<=0
nên -3<=x<=1/2
b: \(\left(2x-7\right)\left(4-5x\right)>=0\)
=>(2x-7)(5x-4)<=0
=>4/5<=x<=7/2
i: \(\Leftrightarrow\dfrac{3-x+2}{x-2}>0\)
\(\Leftrightarrow\dfrac{x-5}{x-2}< 0\)
=>2<x<5


/x-1/+x-2/=1 (1)
Bảng xét dấu:
| x | 1 | 2 | ||
| x-1 | -0 | + | bạn kéo 1 gạch đứng | + |
| x-2 | - bạn kéo 1 gạch đứng nha! | - | 0 | + |
TH1: x<1 thì (1) <=> 1-x+2-x=1
-2x + 3 = 1
- 2x = -1
x = 1 (KTM)
TH2:với 1< hoặc = x bé hơn hoặc = 2 thì ta có:
(1) <=> x-1+2-x=1
0x + 1 = 1
0x = 0 ( vô lý ) => (KTM)
TH3: với x>2 thì ta có:
(1) <=> x-1+x-2=1
2x -3 = 1
2x = 4
x = 2
vậy k có giá trị nào thỏa mãn
\(\Leftrightarrow|^{ }_{ }x-1|^{ }_{ }+|^{ }_{ }2-x|^{ }_{ }=1\)
co \(|^{ }_{ }x-1|^{ }_{ }\ge x-1\)voi moi x
\(|^{ }_{ }2-x|^{ }_{ }\ge2-x\)voi moi x
\(\Rightarrow|^{ }_{ }x-1|^{ }_{ }+|^{ }_{ }2-x|^{ }_{ }\ge x-1+2-x=1\)
dau bang xay ra \(\Leftrightarrow\hept{\begin{cases}x-1\ge0\\2-x\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge1\\x\le2\end{cases}}\Leftrightarrow1\le x\le2\)

để có thể lập đc bảng xét dấu..., bạn cần nắm vững Định lý về dấu của tam thức bậc 2 như f(x)=ax2+bx+cf(x)=ax2+bx+c
những bài toán về xét dấu thì thường có dạng:f(x).g(x)≥0f(x).g(x)≥0 hoặc f(x).g(x)≤0f(x).g(x)≤0 .....v....v
do đó công việc xét dấu của biểu thức xem nó dương hay âm trong khoảng nào trên R, từ đó suy ra tập nghiệm bpt...
Công việc cần làm ở đây là tìm đc nghiệm của tam thức bậc 2, sau đó áp dụng định lý về dấu của tam thức để lập bảng xét dấu....
- cứ ngoài khoảng 2 nghiệm thì cùng dấu với a, trong khoảng 2 nghiệm thì ngược dấu với a....., từ đó tìm đc dấu của f(x),g(x).....=> dấu của f(x).![[IMG]](http://i522.photobucket.com/albums/w341/shinichi_kudo_ha_hd/geuq.gif)
ở vd trên:
trên TXĐ D:
f(x) dương, g(x) âm =>f(x).g(x) âm
f(x) dương, g(x) dương=>f(x).g(x) dương....v..v...