Giải phương trình nghiệm nguyên sau:
23x+53y=109
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BH
1
DD
Đoàn Đức Hà
Giáo viên
15 tháng 1 2023
a) \(\left(5,11\right)=1\) nên phương trình có vô số nghiệm.
Phương trình có một nghiệm là \(\left(3;1\right)\) nên nghiệm tổng quát của phương trình trên là
\(\left\{{}\begin{matrix}x=3+11t\\y=1+5t\end{matrix}\right.\), \(t \in \mathbb{Z}\).
b) \(\left(7,5\right)=1\) nên phương trình có vô số nghiệm.
Phương trình có một nghiệm là \(\left(4;23\right)\) nên nghiệm tổng quát của phương trình trên là
\(\left\{{}\begin{matrix}x=4+5t\\y=23-7t\end{matrix}\right.\), \(t \in \mathbb{Z}\).
c) Bạn đọc tự giải.
NN
2
NL
4 tháng 3 2016
ý bạn a và b là 1 hệ pt hả chứ để riêng sao giải. Nếu giải hệ thì là như sau:
5x-y=13<=> y=5x-13. Thay vào pt b ta có: 23x+53(5x-13)=109 <=> 23x+265x=109+53.13. đến đây bạn tự giải
PG
1
16 tháng 10 2019
a) \(2x+3y+5z=15\)
Vì (2; 3; 5 ) =1
=> Phương trình sẽ có nghiệm nguyên.
\(pt\Leftrightarrow2x+5z=15-3y\)
Đặt: 15 - 3 y = a
Phương trình trở thành: \(2x+5z=a\) (1)
Phương trình (1) có 1 nghiệm là: x = -2a và z = a
=> Phương trình (1) có ngiệm tổng quát là: x = - 2a - 5t ; z = a + 2t (2)
Thế a = 15 -3y vào (2). Ta có: x = -2 (15-3y ) -5t = -30 + 6y - 5t và z = 15-3y +2t
Vậy phương trình trên có nghiệm:
\(\hept{\begin{cases}x=-30+6y-5t\\z=15-3y+2t\\y,t\in Z\end{cases}}\)
Bài b/ tương tự.
NQ
4
TN
20 tháng 2 2016
23x +53y=109
<=> x = (109 - 53y)/23 = 4 - 2y +(17-7y)/23
x nguyên nên 17-7y= 23m => y = (17-23m)/7 = 2 -3m +(3 - 2m)/7
y nguyên nên: 3 - 2m = 7n => m = (3-7n)/2 = 1 - 3n +(1 -n)/2
m nguyên nên: 1 -n = 2p => n = 1-2p
(m,n,p là số nguyên)
Từ n = 1-2p => m = 1 - 3(1-2p) + p = -2 +7p
=> y = 2 -3(-2+7p) + 1- 2p = 9 -23p
=> x = 4 - 2(9 -23p) -2 +7p = 2 -18 +46p +7p = 53p - 16.
Vậy x = 53p - 16; y = 9 - 23p
OK
1
CM
14 tháng 11 2019
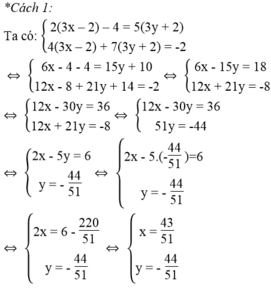
Vậy hệ phương trình đã cho có nghiệm (x; y) = (43/51 ; -44/51 )
*Cách 2: Đặt m = 3x – 2, n = 3y + 2
Ta có hệ phương trình:
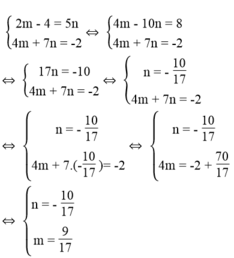
Ta có: 3x – 2 = 9/17 ⇔ 3x = 2 + 9/17 ⇔ 3x = 43/17 ⇔ x = 43/51
3y + 2 = - 10/17 ⇔ 3y = -2 - 10/17 ⇔ 3y = - 44/17 ⇔ y = - 44/51
Vậy hệ phương trình đã cho có nghiệm (x; y) = (43/51 ; -44/51 )
16 tháng 10 2019
Câu hỏi của Phùng Gia Bảo - Toán lớp 9 - Học toán với OnlineMath
HH
2
NH
1 tháng 2 2019
1. Đơn giản hóa
5x + -1y = 13
Giải quyết
5x + -1y = 13
Giải cho biến 'x'.
Di chuyển tất cả các điều khoản có chứa x sang trái, tất cả các điều khoản khác sang phải.
Thêm 'y' vào mỗi bên của phương trình.
5x + -1y + y = 13 + y
Kết hợp như các điều khoản: -1y + y = 0
5x + 0 = 13 + y
5x = 13 + y
Chia mỗi bên cho '5'.
x = 2,6 + 0,2y
Đơn giản hóa x = 2,6 + 0,2y
P/s: Nguồn mạng Oppa :>>
Câu 3 tương tự ((:
\(\Leftrightarrow23x+53y=23.37-53.14\)
\(\Leftrightarrow53y+53.14=23.37-23x\)
\(\Leftrightarrow53\left(y+14\right)=23\left(37-x\right)\)
Do 53 và 23 nguyên tố cùng nhau \(\Rightarrow y+14⋮23\)
\(\Rightarrow y+14=23k\Rightarrow y=23k-14\)
\(\Rightarrow x=-53k+37\)
Vậy nghiệm của pt là \(\left(x;y\right)=\left(-53k+37;23k-14\right)\) với \(k\in Z\)