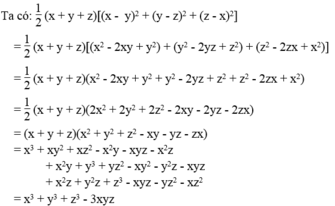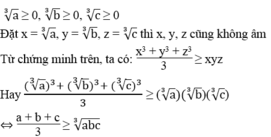Dự đoán đẳng thức xảy ra khi x = y = z = 1.
Đặt x = 1 + a ; y = 1 + b , ( a , b \(\in\) R ). Từ giả thiết suy ra z = 1 - a - b.
Ta có:
\(x^2+y^2+z^2+xy+yz+zx\)\(=\left(1+a\right)^2+\left(1+b\right)^2+\left(1-a-b\right)^2+\left(1+a\right)\left(1+b\right)+\left(1+b\right)\left(1-a-b\right)+\left(1-a-b\right)\left(1+a\right)=\left(a+\frac{b}{2}\right)^2+\frac{3b^2}{4}+6\ge6.\)
Đẳng thức xảy ra khi và chỉ khi.
\(b=0;a+\frac{b}{2}=0\Leftrightarrow a=0;b=0\Leftrightarrow x=y=z=1.\)
Naruto nhận nè bạn.