Câu 1. Cho tam giác ABC vuông tại A (AB<AC). Tia phân giác góc A cắt BC tại D. Trên cạnh AC lấy điểm M sao cho AM=ABa) Chứng minh: DB=DMb) Gọi E là giao điểm AB và MD. Chứng minh \(\Delta BED=\Delta MCD\)c) Gọi H là trung điểm của EC. Chứng minh ba điểm A,D,H thẳng hàngCâu 2 . Cho \(\Delta ABC\)có AB<AC. Tia phân giác góc ABC cắt AC tại D. Trên cạnh BC lấy điểm E sao cho BA=BEa) Chứng minh: DA=DEb) Tia ED cắt BA tại F....
Đọc tiếp
Câu 1. Cho tam giác ABC vuông tại A (AB<AC). Tia phân giác góc A cắt BC tại D. Trên cạnh AC lấy điểm M sao cho AM=AB
a) Chứng minh: DB=DM
b) Gọi E là giao điểm AB và MD. Chứng minh \(\Delta BED=\Delta MCD\)
c) Gọi H là trung điểm của EC. Chứng minh ba điểm A,D,H thẳng hàng
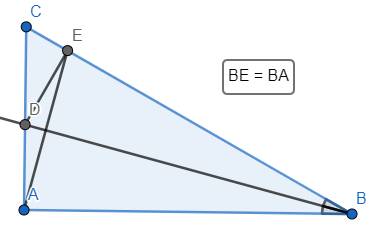
Câu 2 . Cho \(\Delta ABC\)có AB<AC. Tia phân giác góc ABC cắt AC tại D. Trên cạnh BC lấy điểm E sao cho BA=BE
a) Chứng minh: DA=DE
b) Tia ED cắt BA tại F. Chứng minh \(\Delta DAF=\Delta DEC\)
c) Gọi H là trung diểm của FC. Chứng minh ba điểm B,D,H thẳng hàng
Câu 3. Cho \(\Delta ABC\)cân tại A. Kẻ AH vuông góc với BC (\(H\in BC\))
a) Chứng minh: HB=HC
b) Kẻ \(HD\perp AB\left(D\in AB\right)\)và \(HE\perp AC\left(E\in AC\right)\). Chứng minh \(\Delta HDE\)cân
Câu 4. Cho tam giác ABC vuông tại B, đường phân giác \(AD\left(D\in BC\right)\). Kẻ DE vuông góc với \(AC\left(E\in AC\right)\)
a) Chứng minh: \(\Delta ABD=\Delta AED;\)
b) BE là đường trung trực của đoạn thẳng AD
c) Gọi F là giao điểm của hai đường thẳng AB và ED Chứng minh BF=EC


Hình bạn tự vẽ nhé!
Giải:
Vì D là trung điểm của AC (gt)
nên AD = CD
Xét \(\Delta ABD\) và \(\Delta CED\) có:
AD = CD (chứng minh trên)
\(\widehat{ADB}=\widehat{CDE}\)(2 góc đối đỉnh)
ED = BD (gt)
\(\Rightarrow\Delta ABD=\Delta CED\) (c.g.c) (1)
\(\Rightarrow\widehat{ABD}=\widehat{CED}\) (2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow\)AB // CD (dấu hiệu nhận biết) (2)
Từ (1), (2) \(\Rightarrowđpcm\)
b) Ta có: AF _|_ BD tại F
CG _|_ DE tại G
\(\Rightarrow\hept{\begin{cases}\widehat{AFD}=90^o\\\widehat{CGD}=90^o\end{cases}}\Rightarrow\widehat{AFD}=\widehat{CGD}\)
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow\) AF // CG (dấu hiệu nhận biết) (3)
\(\Rightarrow\widehat{FAH}=\widehat{DCG}\) (2 góc so le trong)
Xét \(\Delta ADF\) và \(\Delta CDG\) có:
AD = CD (chứng minh trên)
\(\widehat{ADF}=\widehat{CDG}\) (2 góc đối đỉnh)
\(\widehat{FAH}=\widehat{DCG}\) (chứng minh trên)
\(\Rightarrow\Delta ADF=\Delta CDG\) (g.c.g)
\(\Rightarrow\) DF = DG (2 cạnh tương ứng) (4)
Từ (3), (4) \(\Rightarrowđpcm\)
c) Xét \(\Delta CDE\) có:
Giao điểm 2 đường thẳng CG và EI là M
CG, EI đều là đường cao của \(\Delta CDE\)
\(\Rightarrow\)DM cũng là đường cao của \(\Delta CDE\)
\(\Rightarrow DM\perp AB\)(5)
Xét \(\Delta ABD\) có:
Giao điểm 2 đường thẳng CG, EI là M
AF, BH đều là đường cao của \(\Delta ABD\)
\(\Rightarrow DK\) cũng là đường cao của \(\Delta ABD\)
\(\Rightarrow DK\perp AB\) (6)
Từ (5), (6) suy ra đpcm