Cho a, b, c không âm và a+b+c=3. Tìm MinF=
a
+
b
2
+
c
3
...
Đọc tiếp
Cho a, b, c không âm và a+b+c=3. Tìm MinF= a + b 2 + c 3
K
Khách
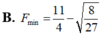
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
P
1
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 2 2022
\(a^3+a^3+1\ge3\sqrt[3]{a^3.a^3.1}=3a^2\)
Tương tự: \(2b^3+1\ge3b^2\) ; \(2c^3+1\ge3c^2\)
\(\Rightarrow2\left(a^3+b^3+c^3\right)+3\ge3\left(a^2+b^2+c^2\right)=9\)
\(\Rightarrow a^3+b^3+c^3\ge3\)
\(A_{min}=3\) khi \(a=b=c=1\)
Lại có: \(\left\{{}\begin{matrix}a;b;c\ge0\\a^2+b^2+c^2=3\end{matrix}\right.\) \(\Rightarrow0\le a;b;c\le\sqrt{3}\)
\(\Rightarrow a^2\left(a-\sqrt{3}\right)\le0\Rightarrow a^3\le\sqrt{3}a^2\)
Tương tự: \(b^3\le\sqrt{3}b^2\) ; \(c^3\le\sqrt{3}c^2\)
\(\Rightarrow a^3+b^3+c^3\le\sqrt{3}\left(a^2+b^2+c^2\right)=3\sqrt{3}\)
\(A_{max}=3\sqrt{3}\) khi \(\left(a;b;c\right)=\left(0;0;\sqrt{3}\right)\) và các hoán vị
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 1
Biểu thức này có vẻ chỉ tìm được min chứ ko tìm được max:
Min:
\(P^2=a+b+c+a^3b^3+b^3c^3+c^3a^3+2\sqrt{\left(a+b^3c^3\right)\left(b+c^3a^3\right)}+2\sqrt{\left(a+b^3c^3\right)\left(c+a^3b^3\right)}+2\sqrt{\left(b+c^3a^3\right)\left(c+a^3b^3\right)}\)
\(P^2\ge a+b+c+2\sqrt{ab}+2\sqrt{bc}+2\sqrt{ca}\ge a+b+c=2\)
\(\Rightarrow P\ge\sqrt{2}\)
\(P_{min}=\sqrt{2}\) khi \(\left(a;b;c\right)=\left(0;0;2\right)\) và các hoán vị
28 tháng 9 2019
Ta có:
\(\frac{\left(a+b+c\right)^2}{3}\le a^2+b^2+c^2=2\left(a+b+c\right)\)
=> \(\left(a+b+c\right)^2-6\left(a+b+c\right)\le0\)
=> \(0\le a+b+c\le6.\)
\(T=\frac{a}{a+1}+\frac{b}{b+a}+\frac{c}{c+1}=1-\frac{1}{a+1}+1-\frac{1}{b+1}+1-\frac{1}{c+1}\)
\(=3-\left(\frac{1}{a+1}+\frac{1}{b+1}+\frac{1}{c+1}\right)\le3-\frac{\left(1+1+1\right)^2}{a+b+c+3}\le3-\frac{3^2}{6+3}=2\)
"=" xảy ra <=> \(a=b=c\)và \(a+b+c=6\)<=> \(a=b=c=2\)
Vậy max T = 2 khi và chỉ khi a=b=c =2
HD
3
6 tháng 3 2020
a,b,c \(\ge\)0 và a + b + c =3 \(\Rightarrow a,b,c< 4\)
giả sử b là số nằm giữa a,c thì ( b - a ) ( b - c ) \(\le\)0
\(\Leftrightarrow b^2+ac\le ab+bc\Rightarrow ab^2+a^2c\le abc+a^2b\)
\(\Rightarrow ab^2+bc^2+ca^2\le abc+a^2b+bc^2\le a^2b+bc^2+2abc=b\left(a+c\right)^2=b\left(3-b\right)^2\)
Cần chứng minh \(b\left(3-b\right)^2\le4\Leftrightarrow b^3-6b^2+9b-4\le0\Leftrightarrow\left(b-1\right)^2\left(b-4\right)\le0\)( luôn đúng )
Vậy GTLN của P là 4 khi ( a,b,c ) là hoán vị của bộ số ( 0 ; 1 ; 2 )
5 tháng 3 2020
1
\(a\sqrt{b^3+1}=a\sqrt{\left(b+1\right)\left(b^2-b+1\right)}\le a\cdot\frac{b+1+b^2-b+1}{2}=\frac{ab^2}{2}+1\)
Tương tự ta có:\(P\le3+\frac{1}{2}\left(ab^2+bc^2+ca^2\right)\)
Giả sử b nằm giữa a và c
Ta có:
\(\left(b-a\right)\left(b-c\right)\le0\Leftrightarrow b^2-bc-ab+ac\le0\Leftrightarrow b^2+ac\le ab+bc\)
\(\Leftrightarrow ab^2+a^2c\le a^2b+abc\Leftrightarrow ab^2+bc^2+ca^2\le a^2b+bc^2+abc\)
\(\le a^2b+bc^2+2abc=b\left(a+c\right)^2=b\left(3-b\right)^2\)
Ta chứng minh \(b\left(3-b\right)^2\le4\) dể chứng minh
Khi đó:\(P\le3+\frac{4}{2}=5\)
Dấu "=" xảy ra tại a=0;b=1;c=2 và các hoán vị
2
Đặt \(a+b-c=x;b+c-a=y;c+a-b=z\)
\(\Rightarrow a=\frac{x+y}{2};b=\frac{y+z}{2};c=\frac{z+x}{2}\)
Bất đẳng thức cần chứng minh tương đương với:\(xyz\le\frac{\left(x+y\right)\left(y+z\right)\left(z+x\right)}{8}\) ( đúng theo bđt cô si )
P/S:a,b,c không là độ dài 3 cạnh tam giác vẫn đúng theo BĐT Schur
5 tháng 3 2020
Bài 1: em làm không đúng rồi và cô không hiểu ý tưởng làm bài của em nhưng có mấy lỗi cơ bản:
Sai dòng thứ nhất \(\frac{ab^2}{2}+a\)
Dấu bằng xảy ra cũng sai. Dòng thứ 6 em nhân cả hai vế cho a mà dấu bằng a = 0 . vô lí
Dòng thứ 5 ( b - a ) ( b - c ) <= 0 thì dấu bằng xảy ra a = b hoặc b = c chứ
Dòng thứ 8 => sau đó làm thế nào.
14 tháng 1 2021
Ta có: \(\sqrt{a^2+b^2+c^2}\ge\sqrt{\dfrac{\left(a+b+c\right)^2}{3}}=\sqrt{3};\sqrt{a^2+b^2+c^2}\le\sqrt{\left(a+b+c\right)^2}=3\).
Đặt \(\sqrt{a^2+b^2+c^2}=t\) \((\sqrt{3}\leq t\leq 3)\).
Ta có: \(P=t+\dfrac{9-t^2}{4}+\dfrac{1}{t^2}=\dfrac{4t^3+9t^2-t^4+4}{4t^2}\).
\(\Rightarrow P-\dfrac{28}{9}=\dfrac{\left(3-t\right)\left(9t^3-9t^2+4t+12\right)}{36}\).
Do \(\sqrt{3}\le t\le3\) nên \(3-t\geq 0\); \(9t^3-9t^2+4t+12>4t+12>0\).
Nên \(P\ge\dfrac{28}{9}\).
Đẳng thức xảy ra khi t = 3, tức (a, b, c) = (0; 0; 3) và các hoán vị.
Vậy...
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 3 2023
Do \(0\le a;b;c\le2\)
\(\Rightarrow abc+\left(2-a\right)\left(2-b\right)\left(2-c\right)\ge0\)
\(\Leftrightarrow2\left(ab+bc+ca\right)-4\left(a+b+c\right)+8\ge0\)
\(\Leftrightarrow2\left(ab+bc+ca\right)\ge4\)
\(\Leftrightarrow\left(a+b+c\right)^2-\left(a^2+b^2+c^2\right)\ge4\)
\(\Leftrightarrow9-\left(a^2+b^2+c^2\right)\ge4\)
\(\Leftrightarrow a^2+b^2+c^2\le5\)
Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(0;1;2\right)\) và các hoán vị
AH
Akai Haruma
Giáo viên
12 tháng 2 2022
Lời giải:
Tìm min:
Áp dụng BĐT AM-GM:
$a^3+a^3+1\geq 3a^2$
$b^3+b^3+1\geq 3b^2$
$c^3+c^3+1\geq 3c^2$
$\Rightarrow 2(a^3+b^3+c^3)+3\geq 3(a^2+b^2+c^2)$
$\Leftrightarrow 2P+3\geq 9$
$\Leftrightarrow P\geq 3$
Vậy $P_{\min}=3$ khi $(a,b,c)=(1,1,1)$
----------------
Tìm max:
$a^2+b^2+c^2=3\Rightarrow a^2,b^2,c^2\leq 3$
$\Rightarrow a,b,c\leq \sqrt{3}$
Do đó: $a^3-\sqrt{3}a^2=a^2(a-\sqrt{3})\leq 0$
$\Rightarrow a^3\leq \sqrt{3}a^2$
Tương tự với $b,c$ và cộng theo vế:
$P\leq \sqrt{3}(a^2+b^2+c^2)=3\sqrt{3}$
Vậy $P_{\max}=3\sqrt{3}$ khi $(a,b,c)=(\sqrt{3},0,0)$ và hoán vị.
Chọn B