
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(Ox:\left\{{}\begin{matrix}x=t\\y=0\\z=0\end{matrix}\right.\).
Lấy điểm \(M\left(1;0;0\right)\in Ox\).
\(d\left(A,Ox\right)=\dfrac{\left|\left[\overrightarrow{MA},\overrightarrow{u_{Ox}}\right]\right|}{\left|\overrightarrow{u_{Ox}}\right|}=\sqrt{10}\).
\(d\left(B,Ox\right)=\dfrac{\left|\left[\overrightarrow{MA},\overrightarrow{u_{Ox}}\right]\right|}{\left|\overrightarrow{u_{Ox}}\right|}=\sqrt{10}\)
Do đó hai điểm \(A,B\) cách đều trục \(Ox\).
b) Điểm \(C\in Oz\) nên tọa độ điểm \(C\) có dạng \(\left(0;0;c\right)\).
Tam giác \(ABC\) vuông tại \(C\) nên \(CA\perp CB\)
suy ra \(\overrightarrow{CA}.\overrightarrow{CB}=0\)
\(\Leftrightarrow1.\left(-2\right)-3.1-\left(1+c\right).\left(3-c\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}c=-2\\c=4\end{matrix}\right.\).
c) Mặt phẳng \(\left(Oyz\right)\): \(x=0\).
Hình chiếu của \(A,B\) trên \(\left(Oyz\right)\) lần lượt là \(A'\left(0;-3;-1\right)\), \(B'\left(0;1;3\right)\).
Phương trình hình chiếu của đường thẳng \(AB\) trên \(\left(Oyz\right)\) là phương trình của đường thẳng \(A'B'\).
d) Gọi tọa độ tâm thỏa mãn yêu cầu bài toán là \(I\left(0;a;b\right)\).
Có \(IO=IA=IB\) suy ra
\(a^2+b^2=1^2+\left(a+3\right)^2+\left(b+1\right)^2=2^2+\left(a-1\right)^2+\left(b-3\right)^2\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{-47}{16}\\b=\dfrac{53}{16}\end{matrix}\right.\).

Chọn A.
Ta có
![]()
![]()
Do SA vuông góc với (ABC) nên một VTCP của đường thẳng SA được chọn là
![]()
Đường thẳng SA qua A(1;0;2) và có VTCP u → = ( 3 ; 6 ; - 6 ) nên có phương trình tham số là:
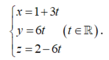
![]()
![]()
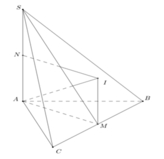
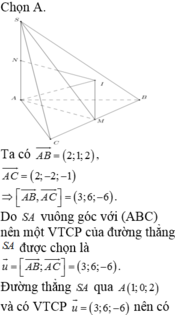
Gọi M là trung điểm BC khi đó M là tâm đường tròn ngoại tiếp tam giác ABC. Gọi d là đường thẳng qua M và song song với AS nên d ⊥ (ABC), suy ra d là trục đường tròn ngoại tiếp tam giác ABC.
Trong mặt phẳng (SAM) vẽ đường trung trực của SA cắt d tại I và cắt SA tại N.
Mặt phẳng (ABC) qua A và có một VTPT
![]()
nên có phương trình tổng quát là:
![]()
![]()
![]()
![]()
![]()
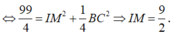
![]()
![]()
![]()
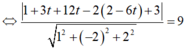
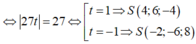
mà cao độ của S âm nên S(4;5;-4) thỏa yêu cầu bài toán.
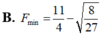
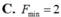
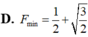
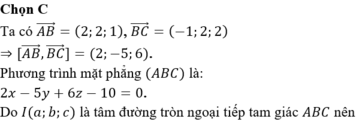
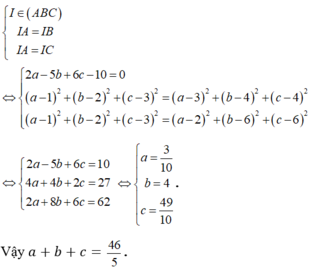

Chọn B