Cho hình chóp S.ABC có SA=SB=SC, góc , , . Tính góc giữa đường thẳng SB và mặt phẳng (ABC).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
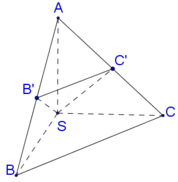
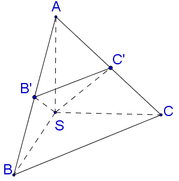
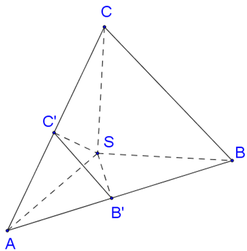
Vì SA=SB=SC suy ra tam giác SAB và tam giác SAC cân tại S. Vậy B′,C′ lần lượt là trung điểm của AB,AC.
Ta có:
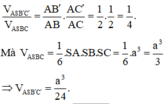

Chọn C
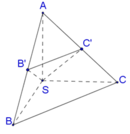
Vì SA=SB=SC suy ra tam giác SAB và tam giác SAC cân tại S. Vậy B′,C′ lần lượt là trung điểm của AB,AC
Ta có
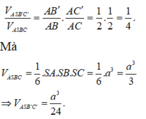

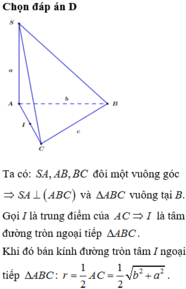
Đáp án D
Đặt SA = SB = SC = a ⇒ ∆ S A C đều cạnh a ⇒ A C = a , A B = a 2
Mặt khác B C 2 = S B 2 + S C 2 - 2 S B . S C . cos 120 ° = 2 a 2 - 2 a 2 . - 1 2 = 3 a 2 ⇒ B C = a 3 .
Khi đó ∆ A B C cận tại A, do SA = SB = SC ⇒ hình chiếu vuông góc của S lên mặt phẳng (ABC) là tâm đường tròn ngoại tiếp tam giác ABC và là trung điểm của cạnh huyền BC.

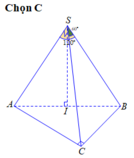
Đáp án B
Ta có: S I ⊥ A B C ⇒ ∆ S I A = ∆ S I B = ∆ S I C (cạnh huyền- cạnh góc vuông)
Suy ra IA = IB = IC hay I là tâm đường tròn ngoại tiếp tam giác ABC.
Đặt SA = SB = SC = x ⇒ B C = x 3 A C = x A B = x 2 ⇒ ∆ A B C vuông tại A do A B 2 + A C 2 = B C 2
Do đó I là trung điểm của BC.

Chọn C.
Phương pháp: Sử dụng công thức tính thể tích khối chóp khi biết ba góc ở một đỉnh và ba cạnh ở đỉnh đó.
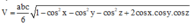
(trong đó a, b, c là độ dài ba cạnh, x, y, z là số đo ba góc ở một đỉnh)
Sau đó tính khoảng cách dựa vào công thức tính thể tích h = 3 V h .
Cách giải: Áp dụng công thức trên ta có:
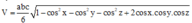
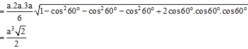

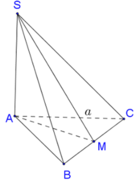

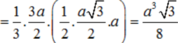

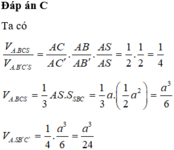


Đáp án C
Đặt SA=a.
=> tam giác ABC vuông tại B.
Gọi O là trung điểm của AC, khi đó OA=OB=OC => S, O cùng thuộc trục của đường tròn ngoại tiếp tam giác ABC, suy ra S O ⊥ ( A B C ) Do đó OB là hình chiếu vuông góc của SB lên mặt phẳng (ABC) nên góc giữa SB và (ABC) là: