Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(\dfrac{V_{SAMC}}{V_{SABC}}=\dfrac{SM}{SB}\)
Theo hệ thức lượng: \(SA^2=SM.SB\Rightarrow SM=\dfrac{SA^2}{SB}\)
\(\Rightarrow\dfrac{SM}{SB}=\left(\dfrac{SA}{SB}\right)^2\)
\(\Rightarrow V_{SAMC}=\left(\dfrac{SA}{SB}\right)^2.V\)
2.
Ta có: \(\dfrac{V_{SAMN}}{V_{SABC}}=\dfrac{SN}{SC}.\dfrac{SM}{SB}\)
Theo c/m câu a ta có \(\dfrac{SM}{SB}=\left(\dfrac{SA}{SB}\right)^2\)
Tương tự áp dụng hệ thức lượng cho tam giác vuông SAC:
\(SA^2=SN.SC\Rightarrow SN=\dfrac{SA^2}{SC}\Rightarrow\dfrac{SN}{SC}=\left(\dfrac{SA}{SC}\right)^2\)
\(\Rightarrow V_{SAMN}=\left(\dfrac{SA}{SB}\right)^2.\left(\dfrac{SA}{SC}\right)^2.V\)

Chọn B.
Dễ thấy AB ⊥ BC. Suy ra SB ⊥ BC, ∆ SMN đồng dạng với ∆ SCB, do đó
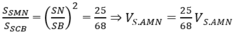

Chọn C.
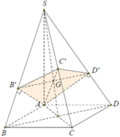
Dễ thấy BD ⊥ SC, nên BD // (AB'C'D'), suy ra BD // B'D'.
Gọi I = AC ∩ BD, J = AC' ∩ SI, khi đó J là trọng tâm của tam giác SAC và J ∈ B'D'.
Suy ra
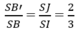
Do đó dễ thấy
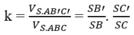
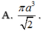


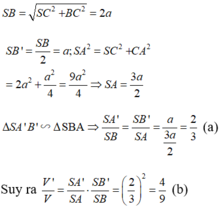

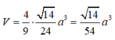
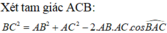




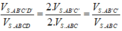
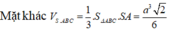
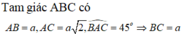

Chọn C
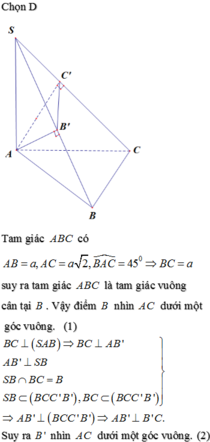
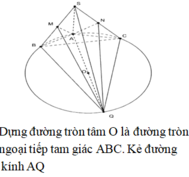
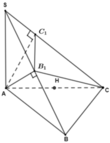
Vì SA=SB=SC suy ra tam giác SAB và tam giác SAC cân tại S. Vậy B′,C′ lần lượt là trung điểm của AB,AC
Ta có