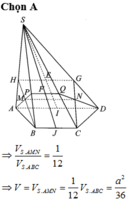
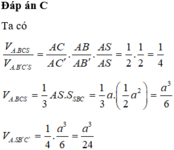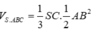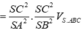Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
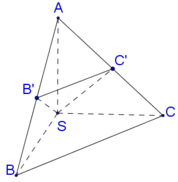
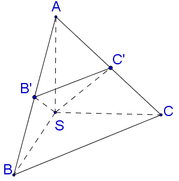
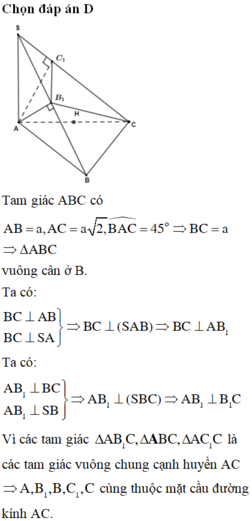
Vì SA=SB=SC suy ra tam giác SAB và tam giác SAC cân tại S. Vậy B′,C′ lần lượt là trung điểm của AB,AC.
Ta có:
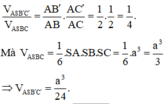
Phương pháp:
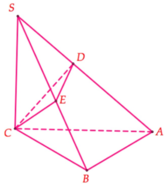
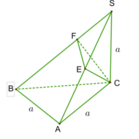
+) Thể tích của tứ diện vuông có độ dài các cạnh góc vuông là a, b, c là: V = 1 6 a b c
+) Sử dụng công thức tỉ số thể tích Simpson
Cách giải:
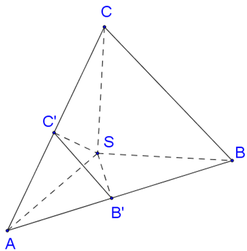
S.ABC là tứ diện vuông tại đỉnh S
và áp dụng tỷ số thể tích có 
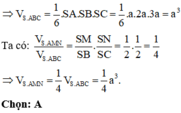
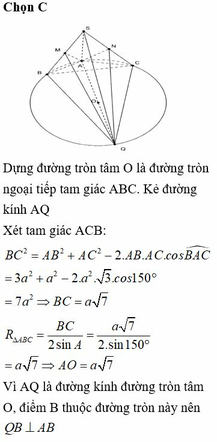
Đáp án A
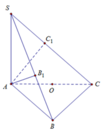
Dễ thấy Δ A B C là tam giác vuông cân tại B, do đó O A = O B = O C (với O là trung điểm của AC)
Ta có B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ A B 1 , lại do A B 1 ⊥ S B ⇒ A B 1 ⊥ B 1 C
Do đó Δ A B 1 C vuông tại O nên O A = O C = O B 1
Vậy O là tâm mặt cầu ngoại tiếp hình chóp A B C C 1 B 1
Do đó R = A C 2 = a 2 2 ⇒ V = 4 3 π R 3 = π a 3 2 3