Cho hàm số y = f ( x ) = ax 3 + bx 2 + cx + d có hai cực trị x 1 , x 2 thỏa - 2 < x 1 < 0 < x 2 < 2 và có đồ thị như hình vẽ.
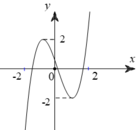
Số điểm cực tiểu của hàm số ![]() là
là
A. 3.
B. 5.
C. 7.
D. 4.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(f\left(-1\right)=2\Rightarrow-a+b-c+d=2\\ f\left(0\right)=1\Rightarrow d=1\\ f\left(1\right)=7\Rightarrow a+b+c+d=7\\ f\left(\dfrac{1}{2}\right)=3\Rightarrow\dfrac{1}{8}a+\dfrac{1}{4}b+\dfrac{1}{2}c+d=3\)
\(d=1\Rightarrow-a+b-c=1;a+b+c=6\\ \Rightarrow2b=7\\ \Rightarrow b=\dfrac{7}{2}\\ \Rightarrow\dfrac{1}{8}a+\dfrac{7}{8}+\dfrac{1}{2}c=2\\ \Rightarrow\dfrac{1}{2}\left(\dfrac{1}{4}a+\dfrac{7}{4}+c\right)=2\\ \Rightarrow\dfrac{1}{4}a+\dfrac{7}{4}+c=4\\ \Rightarrow a+7+4c=16\\ \Rightarrow a+4c=9;a+c=6-\dfrac{7}{2}=\dfrac{5}{2}\\ \Rightarrow3c=\dfrac{13}{2}\Rightarrow c=\dfrac{13}{6}\\ \Rightarrow a=\dfrac{5}{2}-\dfrac{13}{6}=\dfrac{1}{3}\)
Vậy \(\left(a;b;c;d\right)=\left(\dfrac{1}{3};\dfrac{7}{2};\dfrac{13}{6};1\right)\)

Ta có \(f'\left(x\right)=3ax^2+2bx+c;f"\left(x\right)=6ax+2b\)
Hàm số \(f\left(x\right)\) đạt cực tiểu tại \(x=0\) khi và chỉ khi
\(\begin{cases}f'\left(0\right)=0\\f"\left(0\right)>0\end{cases}\)\(\Leftrightarrow\begin{cases}c=0\\2b>0\end{cases}\)\(\Leftrightarrow\begin{cases}c=0\\b>0\end{cases}\left(1\right)\)
Hàm số \(f\left(x\right)\) đạt cực đại tại \(x=1\) khi và chỉ khi \(\begin{cases}f'\left(1\right)=0\\f"\left(1\right)< 0\end{cases}\)\(\Leftrightarrow\begin{cases}3a+2b+c=0\\6a+2b< 0\end{cases}\)
\(\begin{cases}f\left(0\right)=0\\f\left(1\right)=1\end{cases}\)\(\Leftrightarrow\begin{cases}d=0\\a+b+c+d=1\end{cases}\) \(\Leftrightarrow\begin{cases}d=0\\a+b+c+d=1\end{cases}\) (3)
Từ (1), (2), (3) suy ra \(a=-2;b=3;c=0;d=0\)
Kiểm tra lại \(f\left(x\right)=-2x^3+3x^2\)
Ta có \(f'\left(x\right)=-6x^2+6x;f"\left(x\right)=-12x+6\)
\(f"\left(0\right)=6>0\), hàm số đạt cực tiểu tại \(x=0\)
\(f"\left(1\right)=-6< 0\), hàm số đạt cực đại tại \(x=1\)
Vậy \(a=-2;b=3;c=0;d=0\)

Đặt \(g\left(x\right)=2014x\).
Ta có \(f\left(1\right)-g\left(1\right)=0;f\left(2\right)-g\left(2\right)=0;f\left(3\right)-g\left(3\right)=0\).
Do đó \(f\left(x\right)-g\left(x\right)=\left(x-1\right)\left(x-2\right)\left(x-3\right)Q\left(x\right)\).
\(f\left(x\right)=2014x+\left(x-1\right)\left(x-2\right)\left(x-3\right)Q\left(x\right)\).
Do f(x) có bậc 4, hệ số cao nhất là 1 nên Q(x) là đa thức có dạng x + m.
Từ đó \(f\left(x\right)=2014x+\left(x-1\right)\left(x-2\right)\left(x-3\right)\left(x+m\right)\)
\(\Rightarrow f\left(-1\right)+f\left(5\right)=2014.\left(-1\right)+\left(-2\right).\left(-3\right).\left(-4\right)\left(m-1\right)+2014.5+4.3.2\left(m+5\right)=12228\).
Suy ra số điểm cực tiểu của hàm số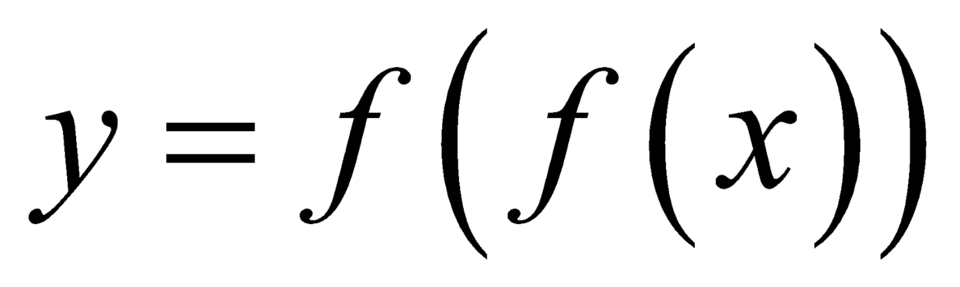 là 4
là 4