So sánh: A = 10 10 + 1 10 11 + 1 v à B 10 9 + 1 10 10 + 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A< \frac{\left(10^{10}-1\right)+11}{\left(10^{11}-1\right)+11}< \frac{10^{10}+10}{10^{11}+10}< \frac{10\left(10^9+1\right)}{10\left(10^{10}+1\right)}< \frac{10^9+1}{10^{10}+1}\)
\(\Rightarrow A< B\)
Vậy A<B

\(A=\dfrac{5^{10}+1}{5^{11}+1}\)
=>\(5\cdot A=\dfrac{5^{11}+5}{5^{11}+1}=\dfrac{5^{11}+1+4}{5^{11}+1}=1+\dfrac{4}{5^{11}+1}\)
\(B=\dfrac{5^9+1}{5^{10}+1}\)
=>\(5B=\dfrac{5^{10}+5}{5^{10}+1}=1+\dfrac{4}{5^{10}+1}\)
\(5^{11}+1>5^{10}+1\)
=>\(\dfrac{4}{5^{11}+1}< \dfrac{4}{5^{10}+1}\)
=>\(\dfrac{4}{5^{11}+1}+1< \dfrac{4}{5^{10}+1}+1\)
=>5A<5B
=>A<B

10A=1011-10/1011-1
=1011-1-9/1011-1
=1 - 9/1011-1
10B=1010-10/1010-1
=1010-1-9/1010-1
=1 - 9/1010-1
Vì 9/1011-1<9/1010-1 nên 1 - 9/1011-1>1 - 9/1010-1
hay 10A>10B
=>A>B(vì 10>0)
\(A=\frac{10^{10}-1}{10^{11}-1}\)
Nhân cả hai vế của A với 10 ta có
\(10A=\frac{10\times\left(10^{10}-1\right)}{10^{11}-1}\)
\(10A=\frac{10^{11}-10}{10^{11}-1}\)
\(10A=\frac{10^{11}-1+9}{10^{11}-1}\)
\(10A=\frac{10^{11}-1}{10^{11}-1}+\frac{9}{10^{11}-1}=1+\frac{9}{10^{11}-1}\left(1\right)\)
\(B=\frac{10^9-1}{10^{10}-1}\)
Nhân cả hai vế của B với 10 ta có
\(10B=\frac{10\times\left(10^9-1\right)}{10^{10}-1}\)
\(10B=\frac{10^{10}-10}{10^{10}-1}\)
\(10B=\frac{10^{10}-1+9}{10^{10}-1}\)
\(10B=\frac{10^{10}-1}{10^{10}-1}+\frac{9}{10^{10}-1}=1+\frac{9}{10^{10}-1}\left(2\right)\)
\(Từ\left(1\right)và\left(2\right)\Rightarrow1+\frac{9}{10^{11}-1}< 1+\frac{9}{10^{10}-1}\)
\(\Rightarrow10A< 10B\)
Vậy A < B

\(A=\dfrac{10^{11}+1}{10^{12}-1}\)
\(\Rightarrow10A=\dfrac{10^{11}+1}{10^{12}-1}.10\)
\(\Rightarrow10A=\dfrac{10\left(10^{11}+1\right)}{10^{12}-1}\)
\(\Rightarrow10A=\dfrac{10^{12}-10}{10^{12}-1}\)
\(B=\dfrac{10^{10}+1}{10^{11}+1}\)
\(\Rightarrow10B=\dfrac{10^{10}+1}{10^{11}+1}.10\)
\(\Rightarrow10B=\dfrac{\left(10^{10}+1\right).10}{10^{11}+1}\)
\(\Rightarrow10B=\dfrac{10^{11}+10}{10^{11}+1}\)
Ta thấy:
\(10^{12}-1>10^{12}-10>0\Rightarrow10A< 1\)
\(0< 10^{11}+1< 10^{11}+10\Rightarrow10B>1\)
Mà \(10A< 1;10B>1\)
\(\Rightarrow B>A\).

Lời giải:
a) Xét hiệu \(\frac{a+n}{b+n}-\frac{a}{b}=\frac{(a+n).b-a(b+n)}{b(b+n)}=\frac{n(b-a)}{b(b+n)}\)
Nếu $b>a$ thì $\frac{a+n}{b+n}-\frac{a}{b}>0\Rightarrow \frac{a+n}{b+n}>\frac{a}{b}$
Nếu $b<a$ thì $\frac{a+n}{b+n}-\frac{a}{b}<0\Rightarrow \frac{a+n}{b+n}<\frac{a}{b}$
Nếu $b=a$ thì $\frac{a+n}{b+n}-\frac{a}{b}=0\Rightarrow \frac{a+n}{b+n}=\frac{a}{b}$
b) Rõ ràng $10^{11}-1< 10^{12}-1$.
Đặt $10^{11}-1=a; 10^{12}-1=b; 11=n$ thì: $a< b$; $A=\frac{a}{b}$ và $B=\frac{10^{11}+10}{10^{12}+10}=\frac{a+n}{b+n}$
Áp dụng kết quả phần a:
$b>a\Rightarrow \frac{a+n}{b+n}>\frac{a}{b}$ hay $B>A$

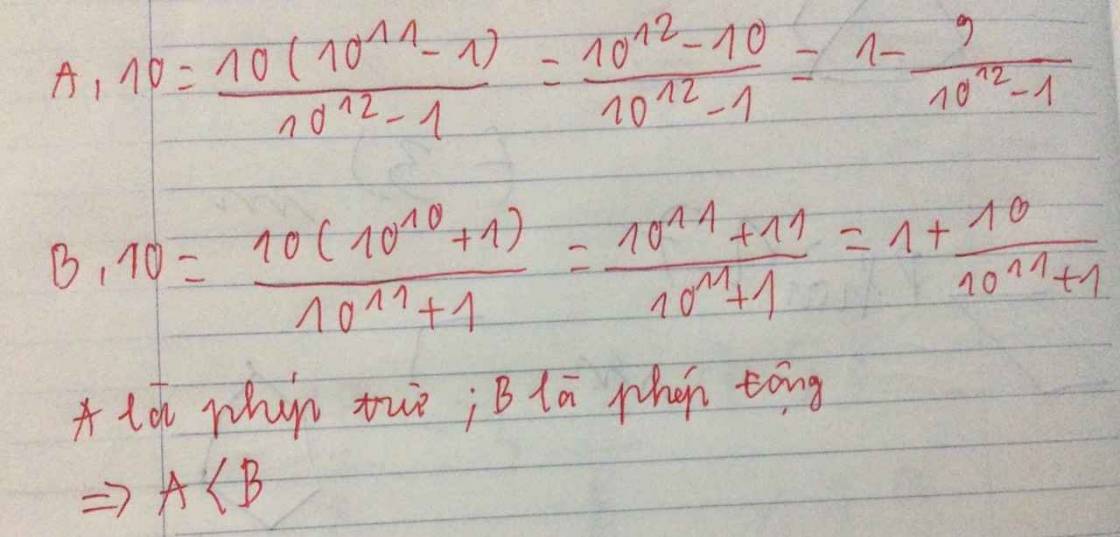
Sử dụng tính chất nếu a b < 1 thì a b < a + m b + m với mọi a, b, m ∈ Z
A = 10 10 + 1 10 11 + 1 < 10 10 + 10 10 11 + 10 = 10 9 + 1 10 10 + 1 = B
Vậy A < B
Cách khác: 10A= 10 11 + 10 10 11 + 1 = 1 + 9 10 11 + 1
10 B = 10 10 + 10 10 10 + 1 = 1 + 9 10 11 + 1 mà 9 10 11 + 1 < 9 10 10 + 1 => A < B