Cho nửa đuuongf tròn(0;R)đường kính AB, từM là 1 điểm trên nửa đường tròn vẽ tiếp tuyến xy.Vẽ AH,BK vuông góc với xy.
Tính AH+BK theo R
Chứng minh AB là tiếp tuyến của đường tròn đường kínHK
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi I là giao điểm của SO với đường tròn.
theo tính chất hai tiếp tuyến cắt nhau ,ta có:
\(\widehat{AOS}=\widehat{SOD}\)\(=sđ\widebat{AI}=sđ\widebat{ID}\)
mà \(\widehat{ABD}=\frac{sđ\widebat{AD}}{2}=sđ\widebat{AI}\)
\(\Rightarrow\widehat{AOS}=\widehat{ABD}\)(đồng vị)
\(\Rightarrow SO//BD\)

Gợi ý:
a) \(DO\) song song với \(EC\) do chúng cùng vuông góc với \(BE\).
b) \(\Delta AEO\sim\Delta ABD\left(g.g\right)\Rightarrow\dfrac{AE}{AB}=\dfrac{AO}{AD}\Rightarrow AO.AB=AE.AD\).
c) \(B,O,E,N\) cùng thuộc đường tròn đường kính \(BN\) do \(\widehat{BON}=\widehat{BEN}=90^o\).
Mà \(B,O,E,D\) cùng thuộc đường tròn đường kính \(OD\) do \(\widehat{DBO}=\widehat{OED}=90^o\)
nên \(B,O,E,N,D\) cùng thuộc một đường tròn
và \(BN,OD\) cắt nhau tại trung điểm mỗi đường.
Suy ra tứ giác \(BOND\) là hình bình hành.
Từ đó suy ra tứ giác \(ODNC\) là hình bình hành.

Gọi N là giao điểm của AD và BC; H là giao điểm của MN và AB
Chứng minh góc AHM= 90; mà góc CAB 45(gt) nên tam giác AHM vuông cân
=>MH = AH
=>MH + HB = AH + HB = 2R (1)
* Tam giác MHB vuông tại H
HB = MB.cos MBH => MB= \(\frac{HB}{sosMBH}\)=\(\frac{HB}{cos60^0}\)=2HB
MH = MB. sin MBH => MH= MB. sin60=\(\frac{MB\sqrt{3}}{2}=HB\sqrt{3}\)
=> \(HB=\frac{MH}{\sqrt{3}}=\frac{\sqrt{3}MH}{3}\) (2)
Từ (1) và (2) ta có \(MH+\frac{\sqrt{3}MH}{3}=2R\Rightarrow MH=\frac{6R}{3+\sqrt{3}}=\left(3-\sqrt{3}\right)R\)
Vậy \(S=\frac{AB.MH}{2}=\frac{1}{2}.2R\left(3-\sqrt{3}\right)R=\left(3-\sqrt{3}\right)R^2\)
cảm ơn bạn, mình còn rất nhiều bt vì mình đang ôn đội tuyển, mong đc các bạn giúp đỡ

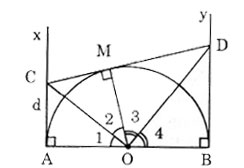 a) Ax ⊥ OA tại A, By ⊥ OB tại B nên Ax, By là các tiếp tuyến của đường tròn.
a) Ax ⊥ OA tại A, By ⊥ OB tại B nên Ax, By là các tiếp tuyến của đường tròn.
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
CM = CA; DM = DB;
∠O1 = ∠O2; ∠O3 = ∠O4
⇒ ∠O2 + ∠O3 = ∠O1 + ∠O4 = 1800/2 = 900 (tính chất hai tia phân giác của hai góc kề bù).
⇒ ∠OCD = 900
b) CM và CA là hai tiếp tuyến của đường tròn, cắt nhau tại C nên CM = CA
Tương tự:
DM = DB
⇒ CM + DM = CA + DB
⇒ CD = AC + BD.
c) Ta có OM ⊥ CD
Trong tam giá vuông COD, OM Là đường cao thuộc cạnh huyển
OM2 = CM.DM
Mà OM = OA = OA = AB/2 và CM = AC; DM = BD
Suy ra AC.BD = AB2/2 = không đổi

a: Xét (O) có
DC,DA là tiếp tuyến
=>DC=DA và OD là phân giác của góc COA
=>OD vuông góc AC
Xét (O) có
EC,EB là tiếp tuyến
=>EB=EC và OE là phân giác của góc COB(2)
=>OE là trung trực của BC
=>OE vuông góc CB
AD+BE=DC+CE=DE
b: Từ (1), (2) suy ra góc DOE=1/2*180=90 độ
Xét tứ giác CMON có
góc CMO=góc CNO=góc MON=90 độ
=>CMON là hình chữ nhật
c: OM*OD+ON*OE
=OC^2+OC^2
=2*R^2ko đổi