Có 6 bạn Hoa, Linh, Trang, Hạnh, Mơ, Thái ngồi quanh một bàn tròn để chơi. Trong đó Hạnh và Hoa không ngồi cạnh nhau. Có bao nhiêu cách xếp 6 bạn này trên bàn tròn nếu tất cả các ghế có phân biệt?
A. 98
B. 72
C. 120
D. 56
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
16 tháng 1 2017
Đúng(0)
Những câu hỏi liên quan
CM
15 tháng 7 2019
a) Xếp 6 nam vào 6 ghế cạnh nhau. Có 6! cách.
Giữa các bạn nam có 5 khoảng trống cùng hai đầu dãy, nên có 7 chỗ có thể đặt ghế cho nữ.
Bây giờ chọn 4 trong 7 vị trí để đặt ghế. Có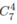 
cách.
Xếp nữ vào 4 ghế đó. Có 4! cách.
Vậy có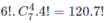 
cách xếp mà không có hai bạn nữ nào ngồi cạnh nhau.
b) Xếp 6 ghế quanh bàn tròn rồi xếp nam vào ngồi. Có 5! cách.
Giữa hai nam có khoảng trống. Xếp 4 nữ vào 4 trong 6 khoảng trống đó. Có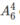 
cách.
Theo quy tắc nhân, có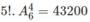 
cách.
CM
5 tháng 9 2019
+ Số cách xếp 8 học sinh nói trên ngồi xung quanh một bạn tròn là 7 !.
+ Đếm số cách xếp 8 học sinh ngồi xung quanh một bàn tròn mà hai học sinh Hải và Liên ngồi cạnh nhau:
Trước tiên, số cách xếp 7 học sinh (trừ bạn Hải sẽ xếp sau) ngồi xung quanh một bàn tròn là 6 !
Khi đó có 2 cách xếp chỗ ngồi cho bạn Hải (ở bên trái hoặc bên phải bạn Liên).
Theo quy tắc nhân, sẽ có 6!.2 cách xếp 8 bạn ngồi xung quanh một bàn tròn mà hai bạn Hải và Liên ngồi cạnh nhau.
Vậy số cách xếp chỗ ngồi sao cho Hải và Liên không ngồi cạnh nhau là: 7! – 6!.2 =6!.5.
Chọn C.
CM
9 tháng 12 2018
Tìm số cách xếp ngẫu nhiên:
Chọn ra 6 trong 12 học sinh rồi xếp vào bàn dài có 
cách xếp;
6 học sinh còn lại xếp vào bàn tròn có (6-1)!=5! cách xếp.
Vậy có tất cả 
cách xếp ngẫu nhiên.
Ta tìm số cách xếp mà A, B cùng ngồi 1 bàn và ngồi cạnh nhau:
TH1: A, B ngồi cùng bàn dài và cạnh nhau có 
cách;
TH2: A, B ngồi cùng bàn tròn và cạnh nhau có 
cách.
Vậy có tất cả 
cách xếp thoả mãn.
Xác suất cần tính bằng
Chọn đáp án B.
*Chú ý số cách xếp n học sinh vào 1 bàn tròn bằng (n−1)! cách.
Chọn đáp án B.
CM
30 tháng 9 2017
Chọn C
Tiến hành theo các bước sau:
Bước 1: Xếp 6 nam ngồi quanh bàn tròn, có 5! Cách xếp.
Bước 2: Vì 6 nam ngồi quanh bàn tròn nên có 6 khoảng trống để xếp 6 người nữ, vậy có 6! Cách xếp.
Theo quy tắc nhân ta có 5!.6! = 86 400 cách.