giúp mình câu 4a với 8a mình cảm ơn ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 8 2016
\(b,=1^2-\left(x-y\right)^2=\left(1+x-y\right)\left(1-x+y\right)\)
11 tháng 8 2016
\(c,=\left(x^2+1\right)^2-\left(2x\right)^2=\left(x^2+2x+1\right)\left(x^2-2x+1\right)=\left(x+1\right)^2\left(x-1\right)^2\)
N
1
28 tháng 10 2021
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{5}=\dfrac{b}{2}=\dfrac{2a-3b}{2\cdot5-3\cdot2}=\dfrac{12}{4}=3\)
Do đó: a=15; b=6
28 tháng 10 2021
d) Áp dụng t/c dtsbn:
\(\dfrac{a}{5}=\dfrac{b}{2}=\dfrac{2a}{10}=\dfrac{3b}{6}=\dfrac{2a-3b}{10-6}=\dfrac{12}{4}=3\)
\(\Rightarrow\left\{{}\begin{matrix}a=3.5=15\\b=3.2=6\end{matrix}\right.\)
f) \(\Rightarrow\dfrac{x}{5}=\dfrac{y}{3}=-\dfrac{z}{2}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{-z}{2}=\dfrac{x+y-z}{5+3+2}=\dfrac{2}{10}=\dfrac{1}{5}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{5}.5=1\\y=\dfrac{1}{5}.3=\dfrac{3}{5}\\z=\dfrac{1}{5}.\left(-2\right)=-\dfrac{2}{5}\end{matrix}\right.\)
g) \(\dfrac{x}{4}=\dfrac{y}{5}=k\)\(\Rightarrow\left\{{}\begin{matrix}x=4k\\y=5k\end{matrix}\right.\)
\(\Rightarrow xy=20k^2=500\Rightarrow k=\pm5\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=20\\y=25\end{matrix}\right.\\\left\{{}\begin{matrix}x=-20\\y=-25\end{matrix}\right.\end{matrix}\right.\)
H
12 tháng 5 2021
a)
$CH_3COOH + KOH \to CH_3COOK + H_2O$
n CH3COOH = n KOH = 0,1(mol)
$CH_3COOH + 2O_2 \xrightarrow{t^o} 2CO_2 + 2H_2O$
$C_2H_5OH + 3O_2 \xrightarrow{t^o} 2CO_2 + 3H_2O$
$CO_2 +C a(OH)_2 \to CaCO_3 + H_2O$
2n C2H5OH + 2n CH3COOH = n CO2 = n CaCO3 = 60/100 = 0,6(mol)
=> n C2H5OH = (0,6 - 0,1.2)/2 = 0,2(mol)
=> n O2 = 2n CH3COOH + 3n C2H5OH = 0,1.2 + 0,2.3 = 0,8(mol)
=> V O2 = 0,8.22,4 = 17,92 lít
b) m = 0,1.60 + 0,2.46 = 15,2 gam
%m CH3COOH = 0,1.60/15,2 .100% = 39,47%
%m C2H5OH = 100%- 39,47% = 60,53%
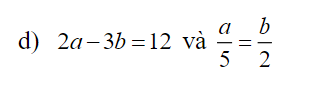
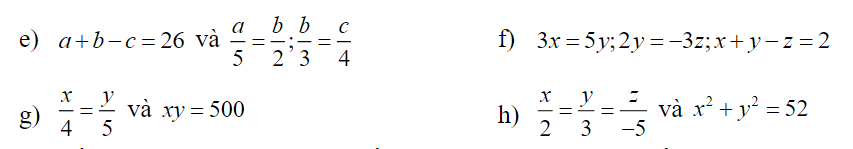
4a.
Do d' là ảnh của d qua phép tịnh tiến nên d' cùng phương d
\(\Rightarrow\) Phương trình d' có dạng: \(x+3y+c=0\)
Lấy \(A\left(1;0\right)\) là 1 điểm thuộc d
\(T_{\overrightarrow{v}}\left(A\right)=A'\Rightarrow\left\{{}\begin{matrix}x'=2+1=3\\y'=0-1=-1\end{matrix}\right.\) \(\Rightarrow A'\left(3;-1\right)\)
Thay tọa độ A' vào pt d' ta được:
\(3+3.\left(-1\right)+c=0\Rightarrow c=0\)
Hay pt d' có dnagj: \(x+3y=0\)
8a.
Đường tròn (C) tâm \(I\left(2;-1\right)\) bán kính \(R=\sqrt{2^2+\left(-1\right)^2+3}=\sqrt{8}\)
Gọi (C') là ảnh của (C) qua phép tịnh tiến, với \(I'\left(x';y'\right)\) và R' lần lượt là tâm và bán kính (C')
Ta có:
\(\left\{{}\begin{matrix}R'=R=\sqrt{8}\\T_{\overrightarrow{v}}\left(I\right)=I'\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x'=2+3=5\\y'=-1+\left(-4\right)=-5\end{matrix}\right.\)
\(\Rightarrow I'\left(5;-5\right)\)
Phương trình (C') có dạng: \(\left(x-5\right)^2+\left(y+5\right)^2=8\)