Giúp toi câu 6 ae ơi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




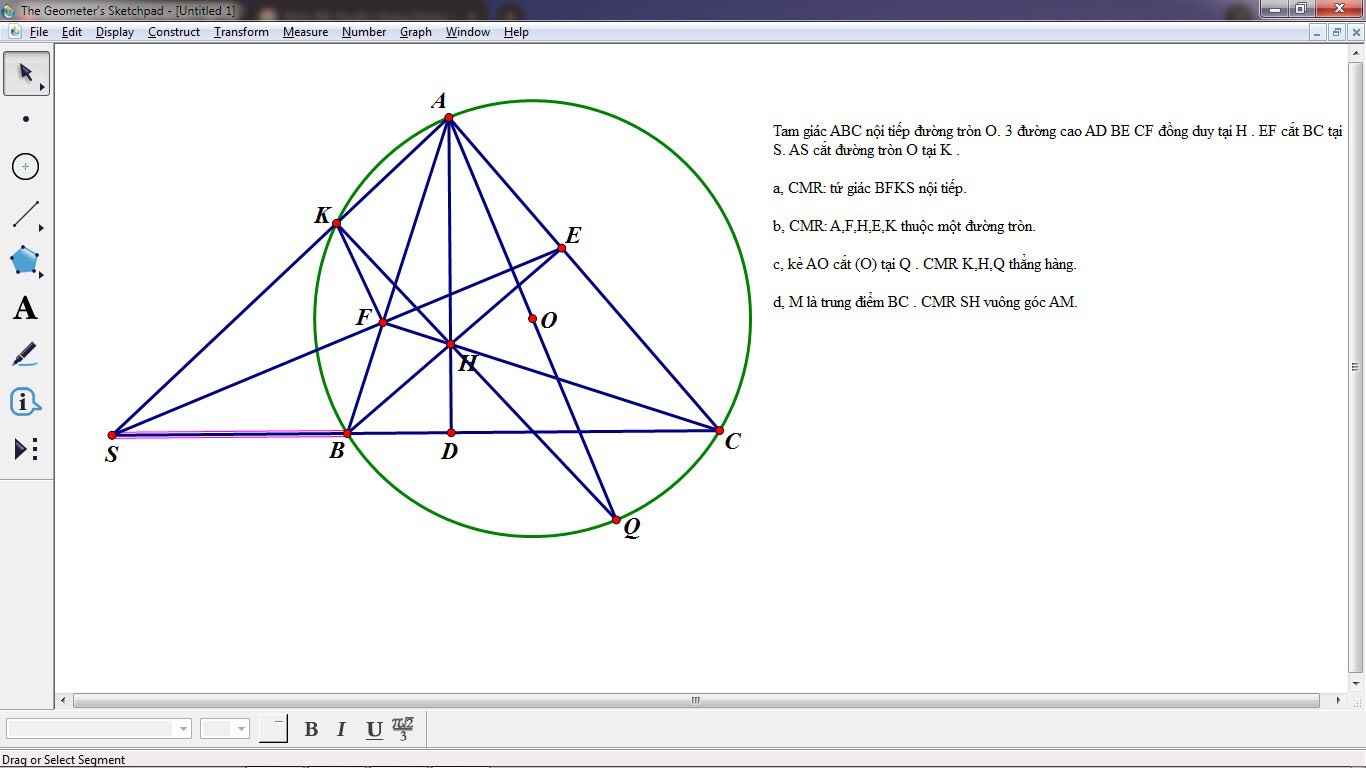
Ta có góc BFH=BDH=90 độ
=> BFHD nội tiếp
=> góc FBH=góc FHA (t/c góc ngoài)(1)
Ta có góc AKH= góc AFH=90 độ
=> AKFH nội tiếp => góc FHA= gócSKF(2)
Từ (1) và (2) => BFKS nội tiếp(t/c góc ngoài)

Bài 1:
b) Ta có: \(\dfrac{x-12}{77}+\dfrac{x-11}{78}=\dfrac{x-74}{15}+\dfrac{x-73}{16}\)
\(\Leftrightarrow\dfrac{x-12}{77}-1+\dfrac{x-11}{78}-1=\dfrac{x-74}{15}-1+\dfrac{x-73}{16}-1\)
\(\Leftrightarrow\dfrac{x-89}{77}+\dfrac{x-89}{78}-\dfrac{x-89}{15}-\dfrac{x-89}{16}=0\)
\(\Leftrightarrow\left(x-89\right)\left(\dfrac{1}{77}+\dfrac{1}{78}-\dfrac{1}{15}-\dfrac{1}{16}\right)=0\)
mà \(\dfrac{1}{77}+\dfrac{1}{78}-\dfrac{1}{15}-\dfrac{1}{16}\ne0\)
nên x-89=0
hay x=89
Vậy: S={89}
Bài 1:
a)ĐKXĐ: \(x\notin\left\{3;-1\right\}\)
Ta có: \(\dfrac{x}{2\left(x-3\right)}+\dfrac{x}{2x+2}=\dfrac{2x}{\left(x-3\right)\left(x+1\right)}\)
\(\Leftrightarrow\dfrac{x\left(x+1\right)}{2\left(x-3\right)\left(x+1\right)}+\dfrac{x\left(x-3\right)}{2\left(x+1\right)\left(x-3\right)}=\dfrac{4x}{2\left(x-3\right)\left(x+1\right)}\)
Suy ra: \(x^2+x+x^2-3x-4x=0\)
\(\Leftrightarrow x^2-6x=0\)
\(\Leftrightarrow x\left(x-6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhân\right)\\x=6\left(nhận\right)\end{matrix}\right.\)
Vậy: S={0;6}

\(M=\sqrt{\dfrac{11+\sqrt{96}}{11-\sqrt{96}}}+\sqrt{\dfrac{11-\sqrt{96}}{11+\sqrt{96}}}\)
\(\Rightarrow M=\sqrt{\dfrac{\left(11+\sqrt{96}\right)^2}{121-96}}+\sqrt{\dfrac{\left(11-\sqrt{96}\right)^2}{121-96}}\)
\(\Rightarrow M=\sqrt{\dfrac{\left(11+\sqrt{96}\right)^2}{25}}+\sqrt{\dfrac{\left(11-\sqrt{96}\right)^2}{25}}\)
\(\Rightarrow M=\dfrac{11+\sqrt{96}}{5}+\dfrac{11-\sqrt{96}}{5}\)
\(\Rightarrow M=\dfrac{22}{5}\)
\(N=\sqrt{15+2\sqrt{15}+2\sqrt{21}+2\sqrt{35}}\\ N=\sqrt{3+5+7+2\sqrt{3}\sqrt{5}+2\sqrt{3}\sqrt{7}+2\sqrt{5}\sqrt{7}}\\ N=\sqrt{\left(\sqrt{3}+\sqrt{5}+\sqrt{7}\right)^2}=\sqrt{3}+\sqrt{5}+\sqrt{7}\)



c) Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE(cmt)
\(\widehat{ADF}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔADF=ΔEDC(cạnh góc vuông-góc nhọn kề)
Suy ra: AF=EC(Hai cạnh tương ứng)
mà AF<DF(ΔADF vuông tại A)
nên EC<DF(đpcm)
d) Xét ΔBFC có
\(\dfrac{BA}{AF}=\dfrac{BE}{EC}\left(BA=BE;AF=EC\right)\)
nên AE//FC(Định lí Ta lét đảo)
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
b) Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABD=ΔEBD(cạnh huyền-góc nhọn)
Suy ra: BA=BE(Hai cạnh tương ứng) và DA=DE(Hai cạnh tương ứng)
Xét ΔABE có BA=BE(cmt)
nên ΔBAE cân tại B(Định nghĩa tam giác cân)
Ta có: BA=BE(cmt)
nên B nằm trên đường trung trực của AE(1)
Ta có: DA=DE(cmt)
nên D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE




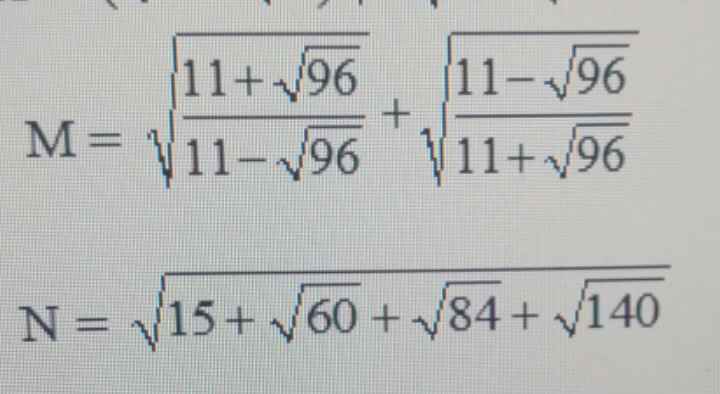

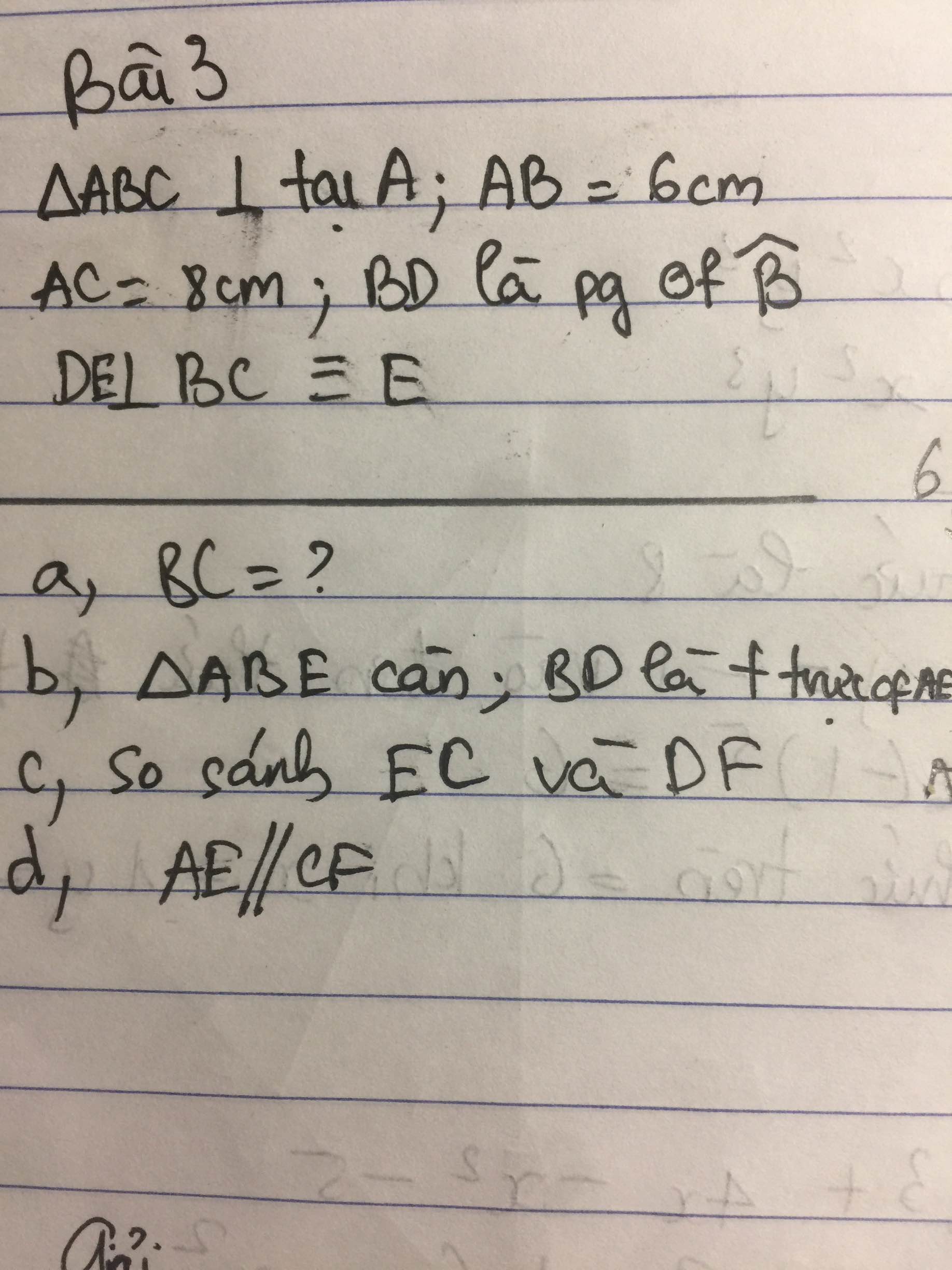
câu hỏi đâu mà giúp