Số giao điểm của đường cong y = x3 – 2x2 + 2x + 1 và đường thẳng y = 1 - x là
A. 1
B. 3
C. 0
D. 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
25 tháng 6 2017
Đúng(0)
Những câu hỏi liên quan
CM
19 tháng 8 2019
Chọn A.
Phương trình hoành độ giao điểm của hai đường trên là:
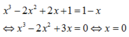
Phương trình có một nghiệm nên đường cong và đường thẳng có một giao điểm
CM
9 tháng 2 2019
Đáp án A
Phương trình hoành độ giao điểm là:
x 3 − 2 x 2 + 2 x + 1 = 1 − x ⇔ x 3 − 2 x 2 + 3 x = 0
⇔ x = 0 do đó 2 đường cong có 1 giao điểm.
CM
28 tháng 3 2018
Đáp án A
Số giao điểm của đường cong và đường thẳng là số nghiệm của phương trình
x 3 - 2 x 2 + 2 x + 1 = 1 - x ⇔ x 3 - 2 x 2 + 3 x = 0 ⇔ x ( x - 1 ) 2 + 2 = 0
⇒ PT có nghiệm duy nhất x=0
PT
1
CM
4 tháng 5 2019
Đáp án C
Xét phương trình
x 3 − 2 x 2 + 2 x + 1 = 1 − x ⇔ x 3 − 2 x 2 + 3 x = 0 ⇔ x = 0 .
Bậy giao điểm của 2 đường cao là (0;1).
CM
10 tháng 1 2017
Đáp án D
Phương trình hoành độ giao điểm x 3 − 2 x 2 − 4 x + 4 = 1 − 2 x có 3 nghiệm phân biệt nên 2 đồ thị có 3 giao điểm.
