. Tìm giá trị nguyên của biến x để biểu thức sau có giá trị là một số...
Đọc tiếp
. Tìm giá trị nguyên của biến x để biểu thức sau có giá trị là một số nguyên
x-2
x+3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
2 tháng 2 2017
Vì 2 / (x - 3) là một số nguyên nên 2 ⋮ (x – 3) và x ≠ 3
Suy ra: x – 3 ∈ Ư(2) = {- 2; - 1; 1; 2}
Ta có:x – 3 = - 2 ⇒ x = 1; x – 3 = - 1 ⇒ x = 2
x – 3 = 1 ⇒ x = 4; x – 3 = 2 ⇒ x = 5
Vậy với x ∈ {1; 2; 4; 5} thì 2 / (x - 3) là một số nguyên.
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
15 tháng 8 2023
\(A=\left(2x+1\right)\left(x^2+1\right)+\dfrac{4}{2x+1}\) (chia đa thức)
Để A nguyên \(\Rightarrow4⋮2x+1\Rightarrow\left(2x+1\right)=\left\{-4;-2;-1;1;2;4\right\}\)
\(\Rightarrow x=\left\{-\dfrac{5}{2};-\dfrac{3}{2};-1;0;\dfrac{1}{2};\dfrac{3}{2}\right\}\)
x thỏa mãn đk đề bài là \(x=\left\{-1;0\right\}\)
LB
2
30 tháng 8 2021
\(\dfrac{2x^3+x^2+2x+2}{2x+1}\left(đk:x\ne-\dfrac{1}{2}\right)=\dfrac{\left(2x+1\right)\left(x^2+1\right)}{2x+1}+\dfrac{1}{2x+1}=x^2+1+\dfrac{1}{2x+1}\)
Do x nguyên nên để biểu thức trên có giá trị nguyên thì :
\(1⋮2x+1\Rightarrow2x+1\inƯ\left(1\right)=\left\{1;-1\right\}\)
\(\Rightarrow x\in\left\{0;-1\right\}\)
30 tháng 8 2021
\(\dfrac{2x^3+x^2+2x+2}{2x+1}\)
\(=\dfrac{2x^3+x^2+2x+1+1}{2x+1}\)
\(=x^2+1+\dfrac{1}{2x+1}\)
Để đó là số nguyên thì \(1⋮2x+1\)
\(\Leftrightarrow2x+1\in\left\{1;-1\right\}\)
\(\Leftrightarrow2x\in\left\{0;-2\right\}\)
hay \(x\in\left\{0;-1\right\}\)
15 tháng 12 2022
Để B nguyên thì \(x^2-2x+4⋮x-2\)
=>\(x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{3;1;4;0;6;-2\right\}\)
AH
Akai Haruma
Giáo viên
15 tháng 12 2022
Lời giải:
Ta có: $B=\frac{x(x-2)+4}{x-2}=x+\frac{4}{x-2}$
Với $x$ nguyên, để $B$ nguyên thì $\frac{4}{x-2}$ nguyên.
Vì $x-2$ nguyên nên $\frac{4}{x-2}$ nguyên khi mà $x-2$ là ước của $4$
$\Rightarrow x-2\in\left\{\pm 1; \pm 2; \pm 4\right\}$
$\Rightarrow x\in\left\{3; 1; 0; 4; 6; -2\right\}$
PT
1
CM
9 tháng 11 2017
Vì 3 / (x + 2) là một số nguyên nên 3 ⋮ (x + 2) và x ≠ - 2
Suy ra: x + 2 ∈ Ư(3) = {- 3; - 1; 1; 3}
Ta có: x + 2 = - 3 ⇒ x = - 5; x + 2= - 1 ⇒ x = - 3
x + 2 = 1 ⇒ x = -1; x + 2 = 3 ⇒ x = 1
Vậy với x ∈ {-5; -3; -1; 1} thì 3 / (x + 2) là một số nguyên.
CM
30 tháng 12 2019
Ta có:
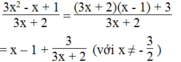
Vì x là số nguyên nên x – 1 là số nguyên.
Để biểu thức đã cho là số nguyên thì 3 ⋮ (3x + 2) và x ≠ -2/3
Suy ra: 3x + 2 ∈ Ư(3) = {-3; -1; 1; 3}
Ta có: 3x + 2 = -3 ⇒ x = -5/3 ∉ Z (loại)
3x + 2 = -1 ⇒ x = - 1
3x + 2 = 1 ⇒ x = -1/3 ∉ Z (loại)
3x + 2 = 3 ⇒ x = 1/3 ∉ Z (loại)
x = -1 khác -3/2
Vậy với x = - 1 thì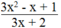
có giá trị nguyên.
CM
9 tháng 2 2018
Ta có:
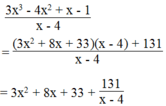
Với x là số nguyên ta có: 3 x 2 + 8 x + 33 là số nguyên.
Để biểu thức đã cho là số nguyên thì 131 ⋮ (x – 4) và x ≠ 4
Suy ra: x – 4 ∈ Ư(131) = {-131; -1; 1; 131}
Ta có: x – 4 = -131 ⇒ x = -127; x – 4 = -1 ⇒ x = 3
x – 4 = 1 ⇒ x = 5; x – 4 = 131 ⇒ x = 135
Vậy với x ∈ {-127; 3; 5; 135} thì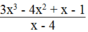 
là số nguyên.
TN
19 tháng 5 2021
a) Ta có: \(M=\dfrac{8x+1}{4x-5}=\dfrac{8x-10+11}{4x-5}=\dfrac{2\left(x-5\right)+11}{4x-5}=2+\dfrac{11}{4x-5}\)
Để M nhận giá trị nguyên thì \(2+\dfrac{11}{4x-5}\) nhận giá trị nguyên
\(\Rightarrow\dfrac{11}{4x-5}\) nhận giá trị nguyên
\(\Rightarrow11⋮4x-5\)
Vì \(x\in Z\) nên \(4x-5\in Z\)
\(\Rightarrow4x-5\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)
\(\Rightarrow x\in\left\{1;\pm1,5;4\right\}\)
Vậy \(x\in\left\{1;4\right\}\) thỏa mãn \(x\in Z\).
b) Ta có: \(A=\dfrac{5}{4-x}\). ĐK: \(x\ne4\)
Nếu 4 - x < 0 thì x > 4 \(\Rightarrow A>0\)
4 - x > 0 thì x < 4 \(\Rightarrow A< 0\)
Để A đạt GTLN thì 4 - x là số nguyên dương nhỏ nhất
\(\Rightarrow4-x=1\Rightarrow x=3\)
\(\Rightarrow A=\dfrac{5}{4-3}=5\)
Vậy MaxA = 5 tại x = 3
c) \(B=\dfrac{8-x}{x-3}\). ĐK: \(x\ne3\).
Ta có: \(B=\dfrac{8-x}{x-3}=\dfrac{-\left(x-8\right)}{x-3}=\dfrac{-\left(x-3\right)+5}{x-3}=\dfrac{5}{x-3}-1\)
Để B đạt giá trị nhỏ nhất thì \(\dfrac{5}{x-3}-1\) nhỏ nhất
\(\Rightarrow\dfrac{5}{x-3}\) nhỏ nhất
Nếu x - 3 > 0 thì x > 3 \(\Rightarrow\dfrac{5}{x-3}>0\)
x - 3 < 0 thì x < 3 \(\Rightarrow\dfrac{5}{x-3}< 0\)
Để \(\dfrac{5}{x-3}\) nhỏ nhất thì x - 3 là số nguyên âm lớn nhất
\(\Rightarrow x-3=-1\Rightarrow x=2\)
\(\Rightarrow B=\dfrac{8-2}{2-3}=-6\)
Vậy MaxB = -6 tại x = 2.
TN
19 tháng 5 2021
Mình làm sai câu a...
Ta có: \(M=\dfrac{8x+1}{4x-1}=\dfrac{8x-2+3}{4x-1}=\dfrac{2\left(4x-1\right)+3}{4x-1}=2+\dfrac{3}{4x-1}\)
Để M nhận giá trị nguyên thì \(2+\dfrac{3}{4x-1}\) nhận giá trị nguyên
\(\Rightarrow\dfrac{3}{4x-1}\) nhận giá trị nguyên
Vì \(4x-1\in Z\) nên \(4x-1\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow x\in\left\{\pm0,5;0;1\right\}\)
Vậy \(x\in\left\{0;1\right\}\) thỏa mãn \(x\in Z\).
Tìm điều kiện của biến x để giá trị của biểu thức P được xác định.
21 tháng 12 2021
a) ĐK:\(\begin{cases} x + 2≠0\\ x - 2≠0 \end{cases}\)⇔\(\begin{cases} x ≠ -2\\ x≠ 2 \end{cases}\)
Vậy biểu thức P xác định khi x≠ -2 và x≠ 2
b) P= \(\dfrac{3}{x+2}\)-\(\dfrac{2}{2-x}\)-\(\dfrac{8}{x^2-4}\)
P=\(\dfrac{3}{x+2}\)+\(\dfrac{2}{x-2}\)-\(\dfrac{8}{(x-2)(x+2)}\)
P= \(\dfrac{3(x-2)}{(x-2)(x+2)}\)+\(\dfrac{2(x+2)}{(x-2)(x+2)}\)-\(\dfrac{8}{(x-2)(x+2)}\)
P= \(\dfrac{3x-6+2x+4-8}{(x-2)(x+2)}\)
P=\(\dfrac{5x-10}{(x-2)(x+2)}\)
P=\(\dfrac{5(x-2)}{(x-2)(x+2)}\)
P=\(\dfrac{5}{x+2}\)
Vậy P=\(\dfrac{5}{x+2}\)
Bài làm
Ta có : \(\frac{x-2}{x+3}=\frac{x+3-5}{x+3}=1-\frac{5}{x+3}\) ( x khác -3 )
Để biểu thức có giá trị nguyên thì \(\frac{5}{x+3}\)đạt giá trị nguyên
=> 5 chia hết cho ( x + 3 )
=> ( x + 3 ) thuộc Ư(5) = { ±1 ; ±5 }
Các giá trị trên đều thỏa mãn ĐKXĐ
Vậy x thuộc { -8 ; -4 ; -2 ; 2 }