B5 Tam giác ABC có AB=4,AC=6 và trung tuyến BM=3.Tính độ dài cạnh BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng công thức trung tuyến:
\(BM^2=\dfrac{2\left(AB^2+BC^2\right)-AC^2}{4}\Rightarrow AC^2=2\left(AB^2+BC^2\right)-4BM^2=16\)
\(\Rightarrow AC=4\)

\(\Delta ABC\)có : AB2 + AC2 = (4,5)2 + 62 = 56,25 = (7,5)2 = BC2 nên\(\Delta ABC\)vuông tại A
=> Trung tuyến AM bằng nửa cạnh huyền BC và bằng : 7,5 : 2 = 3,75 (cm)

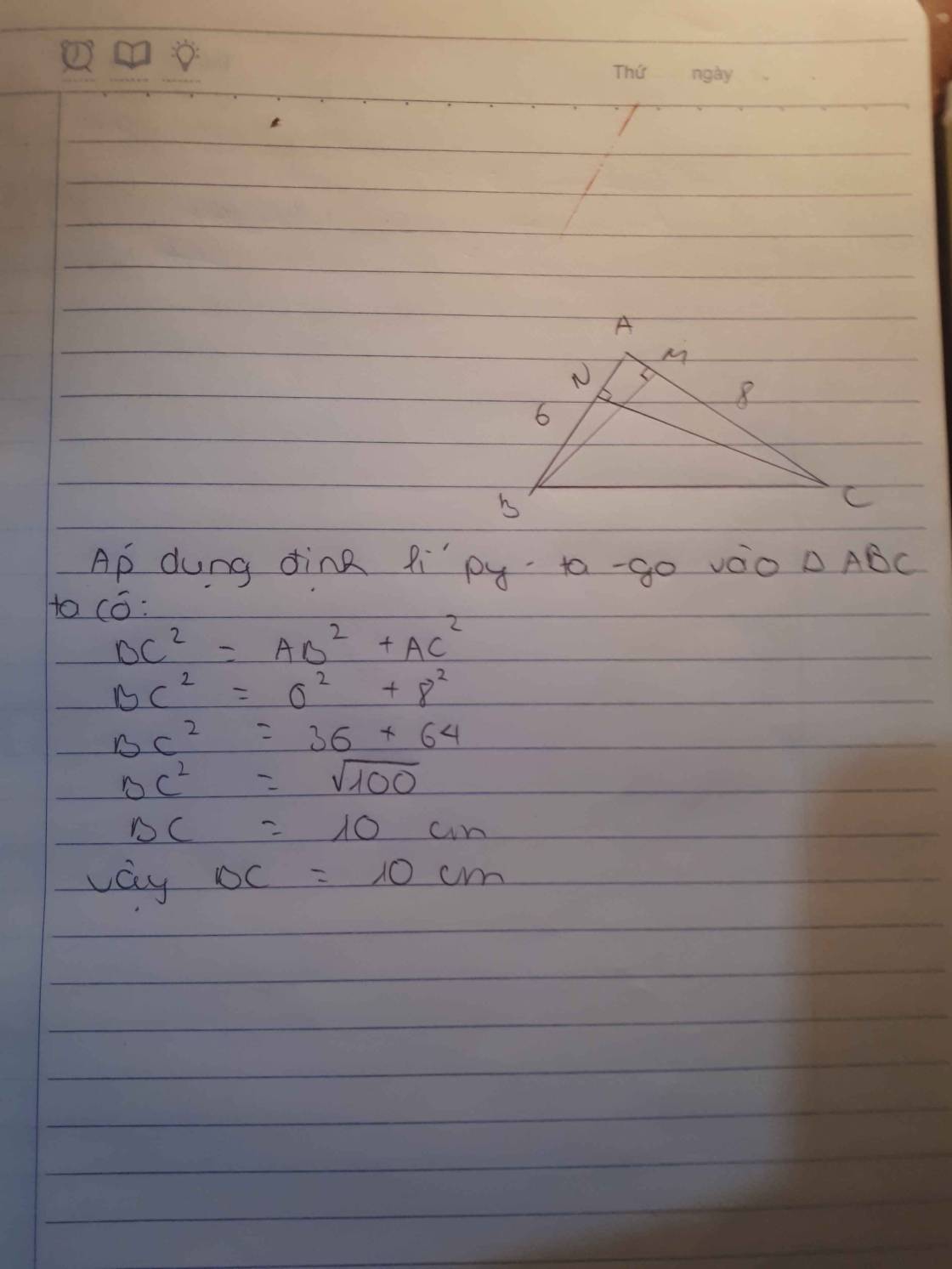
a) Áp dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2=8^2+6^2=100\Rightarrow BC=10\left(cm\right)\)
b) Do \(AD=AB\) nên \(CA\) là trung tuyến
Mà \(AC\cap BK=E\) với \(BK\) là trung tuyến
\(\Rightarrow E\) là trọng tâm \(\Delta BCD\)
\(\Rightarrow CE=\dfrac{2}{3}AC=\dfrac{2}{3}.6=4\left(cm\right)\Rightarrow AE=2\left(cm\right)\)
c) Ta có \(CA\) vừa là trung tuyến vừa là đường cao \(\Delta BCD\)
\(\Rightarrow\Delta BCD\) cân tại \(C\Rightarrow CB=CD\)

Chọn D.
Gọi M là trung điểm của AC suy ra
![]() .
.
Do tam giác BAM vuông tại A
![]()
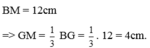
\(b=6;c=4;m_b=3\)
Áp dụng công thức trung tuyến:
\(m_b^2=\frac{a^2+c^2}{2}-\frac{b^2}{4}\Rightarrow a=\sqrt{2m_b^2+\frac{b^2}{2}-c^2}=2\sqrt{5}\)