Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

có \(AB^2+AC^2=BC^2\)
\(4^2+7^2=BC^2\)
\(BC^2=65\)
\(BC=\sqrt{65}\)
ᵈʳᵉᵃᵐ乡๖ۣۜH๖ۣۜA๖ۣۜY๖ۣۜA๖ۣۜT๖ۣۜO sai rồi, đây là tam giác thường, và bạn cx chưa cm là tam giác vuông, nên k sử dunhj đc định lí Ptago đâu/

Tam giác ABC có chu vi bằng 74cm, AC là cạnh lớn nhất. Đường phân giác của góc A chia cạnh BC thành hai đoạn tỉ lệ với 2:3; đường phân giác của góc C chia cạnh AB thành hai đoạn tỉ lệ với 4:5. Tính độ dài các cạnh của tam giác ABC.
AB + BC + AC = 74 (*)
Trong ∆ ABC phân giác AD → AB/AC = DB/DC = 2/3 (AC > AB)
→ AB = 2/3 . AC (1) , tương tự với phân giác CE ta suy ra
BC = 4/5 . AC (2) . Thế tất cả vào (*) ta được:
2/3 . AC + 4/5 . AC + AC = 74 → 37AC/15 = 74 → AC = 30cm
thế vào (1) và (2) ta được AB = 10cm, BC = 24cm

Hạ MH và BK vuông AC,
Ta thấy MH là đường tr.bình t.g BCK.
Có góc BÂK =60 độ
nên KA =AB/2 =2
và BK =2.căn3
=> MH =BK/2 = căn3.
Mặt khác KC =KA +AC =8
=> KH =KC/2 =4
=> AH =2. T
a lại có AM2 =AH^2+HM^2 =4+3 =7
nên AM = √7

Áp dụng định lí Cos : \(BC=\sqrt{AB^2+AC^2-2AB.AC.cos\widehat{BAC}}=\sqrt{4^2+6^2-2.4.6.cos120^o}=2\sqrt{19}\) (cm)
\(AM=\sqrt{\frac{AB^2+AC^2}{2}-\frac{BC^2}{4}}=...\)
2,65 ( làm tròn đến số thập phân số 2)
kết quả đúng mkf thử rồi![]()

Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
B C 2 = A B 2 + A C 2 = a 2 + b 2
Suy ra: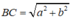
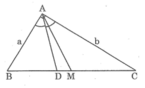
Ta có: AM = BM = 1/2.BC (tính chất đường trung tuyến ứng với cạnh huyền).
Suy ra: AM = 1/2 a 2 + b 2
Vì AD là đường phân giác của ∠(BAC) nên:
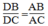 (tính chất đường phân giác)
(tính chất đường phân giác)
Suy ra: 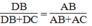
hay 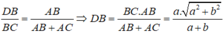
Vậy
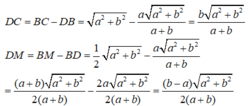
\(\Delta ABC\)có : AB2 + AC2 = (4,5)2 + 62 = 56,25 = (7,5)2 = BC2 nên\(\Delta ABC\)vuông tại A
=> Trung tuyến AM bằng nửa cạnh huyền BC và bằng : 7,5 : 2 = 3,75 (cm)