Từ đỉnh C của ΔABC nhọn, kẻ đường cao CH; kẻ HM ⊥ BC, HN ⊥ AC. CM: ΔMNC đồng dạng với ΔABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 10 2021
Bài 2:
b: \(AH\cdot\left(\cot\widehat{B}+\cot\widehat{C}\right)\)
\(=AH\cdot\left(\dfrac{BH}{AH}+\dfrac{CH}{AH}\right)\)
\(=AH\cdot\dfrac{BC}{AH}=BC\)
CM
21 tháng 2 2018
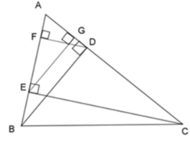
Từ câu trước ta có: A E A B = A G A D => AE.AD = AB.AG (1)
Chứng minh tương tự, ta được: ΔAFD ~ ΔAEC (c - c - c)
=> => AF.AC = AE.AD (2)
Từ (1) và (2) ta có: AD.AE = AB.AG = AC.AF
Đáp án: B
CM
7 tháng 4 2017
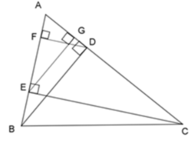
Từ câu trước ta có: A E A B = A G A D = E G B D => AE.AD = AB.AG (1) nên A đúng
Chứng minh tương tự, ta được: ΔAFD ~ ΔAEC (c - c - c)
=> A F A E = A D A C => AF.AC = AE.AD (2) nên B đúng
Ngoài ra A D A C = F D E C => AD.EC = AC.FD nên C đúng
Chỉ có đáp án D sai vì A E E G = A B B D
Đáp án: D
CM
6 tháng 12 2019
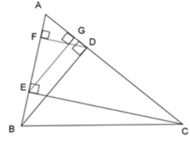
Xét ΔABD và ΔAEG, ta có:
BD ⊥ AC (BD là đường cao)
EG ⊥ AC (EG là đường cao)
=> BD // EG
Theo định lý Talet, ta có: A E A B = A G A D = E G B D
=> ΔAEG đồng dạng ΔABD (c - c - c) (đpcm)
Đáp án: A
30 tháng 4 2019
Xét \(\Delta ABD\)và \(\Delta ACE\)có:
\(\widehat{ADB}=\widehat{AEC}=90^o\); \(\widehat{BAC}\)( chung )
\(\Rightarrow\)\(\Delta ABD\approx\Delta ACE\left(g.g\right)\)
\(\Rightarrow\)\(\frac{AB}{AC}=\frac{AD}{AE}\)
Xét \(\Delta ADE\)và \(\Delta ABC\)có :
\(\frac{AB}{AC}=\frac{AD}{AE}\); \(\widehat{BAC}\)( chung )
\(\Rightarrow\Delta ADE\approx\Delta ABC\left(c.g.c\right)\)
\(\Rightarrow\widehat{D_1}=\widehat{ABC}\)
Xét \(\Delta ADM\)và \(\Delta ABN\)có :
\(\widehat{D_1}=\widehat{ABN}\); \(\widehat{A_1}=\widehat{A_2}\)
\(\Rightarrow\Delta ADM\approx\Delta ABN\left(g.g\right)\)
\(\Rightarrow\frac{AD}{AB}=\frac{AM}{AN}=\frac{1}{2}\)
Vậy M là trung điểm AN
CM
16 tháng 6 2019
Xét ΔABD và ΔAEG, ta có:
BD ⊥ AC (BD là đường cao)
EG ⊥ AC (EG là đường cao)
=> BD // EG
Theo định lý Talet, ta có: A E A B = A G A D = E G B D
=> ΔAEG ~ ΔABD (c - c - c) nên (1) đúng.
Tương tự ta cũng chứng minh được ΔADF ~ ΔACE nên (2) đúng
Dễ thấy (3) sai vì A E A B ≠ A C A C
Vậy có hai cặp tam giác đồng dạng trong các cặp đã nêu.
Đáp án: C
LL
28 tháng 11 2016
a, vì BD song song với AC nên góc B2 bằng góc C2. tương tự được góc C1 bằng góc B1.Do đó tam giác ABC = tam giác BAE(g.c.g) (dpcm)
b, vì AC song song với BD nên góc D bằng góc ACF.
vì AF song song với BC nên góc C1= góc CAF = B2.
theo câu a, tam giác ABC= tam giác DCB nên AC=BD, AB=DC
Do đó tam giác BDC=tam giác ACF(g.c.g) nên DC = CF=AB nên DF= DC+CF=2.AB.
Tương tự ta đc; DE=2.AC, EF=2.BC
Do đó Chu vi tam giác DEF bằng 2 lần chu vi tam giác ABC và bằng 30 cm
