Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


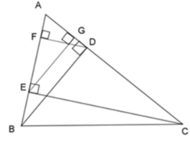
a) \(\Delta\)AGE và \(\Delta\)ADB vuông có ^A chung nên \(\Delta AGE~\Delta ADB\)
\(\Rightarrow\frac{AG}{AD}=\frac{AE}{AB}\Rightarrow AG.AB=AD.AE\)(1)
\(\Delta\)AFD và \(\Delta\)AEC vuông có ^A chung nên\(\Delta AFD~\Delta AEC\)
\(\Rightarrow\frac{AF}{AE}=\frac{AD}{AC}\Rightarrow AF.AC=AE.AD\)(2)
Từ (1) và (2) suy ra AD.AE = AB.AG = AC.AF (đpcm)
b) Ta đã chứng minh AB.AG = AC.AF (câu a)
\(\Rightarrow\frac{AG}{AC}=\frac{AF}{AB}\)
\(\Rightarrow FG//BC\)(Theo định lý Thales đảo)
Vậy FG // BC (đpcm)

Từ câu trước ta có: A E A B = A G A D => AE.AD = AB.AG (1)
Chứng minh tương tự, ta được: ΔAFD ~ ΔAEC (c - c - c)
=> => AF.AC = AE.AD (2)
Từ (1) và (2) ta có: AD.AE = AB.AG = AC.AF
Đáp án: B

a: Xét ΔABD có EG//BD
nên AG/AD=AE/AB
hay \(AG\cdot AB=AE\cdot AD\left(1\right)\)
Xét ΔAEC có FD//EC
nên AF/AE=AD/AC
hay \(AF\cdot AC=AD\cdot AE\left(2\right)\)
Từ (1) và (2)suy ra \(AG\cdot AB=AF\cdot AC=AD\cdot AE\)
b: Xét ΔABC có AF/AB=AG/AC
nên FG//BC

Xét 2 tgiac vuông ADB và AEC có: góc A chung
\(\Rightarrow\Delta ADB\sim\Delta AEC\left(g\right)\Rightarrow\frac{AD}{AE}=\frac{AB}{AC}\left(1\right)\)
Xét 2 tgiac vuông AGE và AFD có góc A chung
\(\Rightarrow\Delta AGE\sim\Delta AFD\left(g\right)\Rightarrow\frac{AG}{AF}=\frac{AE}{AD}\left(2\right)\)
từ (1) và (2) suy ra bạn sai đề câu a
Từ câu trước ta có: A E A B = A G A D = E G B D => AE.AD = AB.AG (1) nên A đúng
Chứng minh tương tự, ta được: ΔAFD ~ ΔAEC (c - c - c)
=> A F A E = A D A C => AF.AC = AE.AD (2) nên B đúng
Ngoài ra A D A C = F D E C => AD.EC = AC.FD nên C đúng
Chỉ có đáp án D sai vì A E E G = A B B D
Đáp án: D