Tìm số tự nhiên n để biểu thức là số chính phương:
n4 + 2n3 + 2n2 + 2n + 7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TV
0
PT
1
CM
4 tháng 11 2019
Điều kiện xác định của phân thức: n ≠ 2
Ta có:
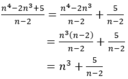
Vậy để N nguyên thì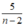 
nguyên ⇒ n – 2 là ước của 5;
Ư
(
5
)
=
-
1
;
1
;
-
5
;
5
n - 2= -1 ⇒ n =1;
n – 2 = 1 ⇒ n =3;
n – 2 = -5 ⇒ n = - 3;
n – 2 = 5 ⇒ n = 7;
vì n ∈ N nên n = 1; n = 3; n = 7
Vậy với n ∈ { 1; 3; 7} thì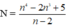 
có giá trị là số nguyên
HT
0
VV
0
HV
1
H
1
6 tháng 6 2015
Để A là số tự nhiên thì 15 chia hết cho 2n+1
\(\Rightarrow\)2n+1\(\inƯ\left(15\right)\)
\(\Rightarrow\)2n+1\(\in\){1,-1,-3,3,5,-5,15,-15}
\(\Rightarrow\)2n\(\in\){0,-2,-4,2,4,-6,14,-16}
\(\Rightarrow\)n\(\in\){0,-1,-2,1,2,-3,7,-8}
