Question

[Truongduy]

Cho f(x) +2f'(x) + f"(x) =x^3 + 2x^2 . biết f(0)=f'(0)=1 . tính tích phân cận 0 đến 1 của f(x)

Answer 1

[Nguyễn Việt Lâm]

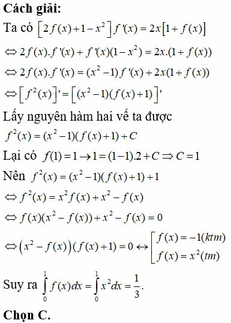
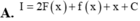
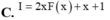
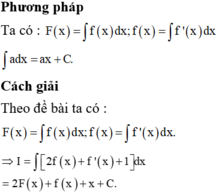
\(f\left(x\right)+2f'\left(x\right)+f''\left(x\right)=x^3+2x^2\)

\(\Leftrightarrow f\left(x\right)+f'\left(x\right)+f'\left(x\right)+f''\left(x\right)=x^3+2x^2\)

\(\Leftrightarrow f\left(x\right)+f'\left(x\right)+\left[f\left(x\right)+f'\left(x\right)\right]'=x^3+2x^2\)

Đặt \(f\left(x\right)+f'\left(x\right)=u\left(x\right)\) ta được:

\(u\left(x\right)+u'\left(x\right)=x^3+2x^2\)

\(\Leftrightarrow e^x.u\left(x\right)+e^x.u'\left(x\right)=e^x\left(x^3+2x^2\right)\)

\(\Leftrightarrow\left[e^x.u\left(x\right)\right]'=e^x\left(x^3+2x^2\right)\)

\(\Rightarrow e^x.u\left(x\right)=\int e^x\left(x^3+2x^2\right)dx=e^x\left(x^3-x^2+2x-2\right)+C\)

\(\Leftrightarrow e^x\left[f\left(x\right)+f'\left(x\right)\right]=e^x\left(x^3-x^2+2x-2\right)+C\)

Thay \(x=0\) vào ta được \(2=-2+C\Rightarrow C=4\)

\(\Rightarrow e^x.f\left(x\right)+e^x.f'\left(x\right)=e^x\left(x^3-x^2+2x-2\right)+4\)

\(\Leftrightarrow\left[e^x.f\left(x\right)\right]'=e^x\left(x^3-x^2+2x-2\right)+4\)

\(\Rightarrow e^x.f\left(x\right)=\int\left[e^x\left(x^3-x^2+2x-2\right)+4\right]dx\)

\(\Rightarrow e^x.f\left(x\right)=e^x\left(x^3-4x^2+10x-12\right)+4x+C_1\)

Thay \(x=0\) vào ta được: \(1=-12+C_1\Rightarrow C_1=13\)

\(\Rightarrow e^x.f\left(x\right)=e^x\left(x^3-4x^2+10x-12\right)+4x+13\)

\(\Rightarrow f\left(x\right)=x^3-4x^2+10x-12+\frac{4x+13}{e^x}\)

\(\Rightarrow\int\limits^1_0f\left(x\right)dx=\int\limits^1_0\left(x^3-4x^2+10x-12\right)dx+\int\limits^1_0\left(4x+13\right).e^{-x}dx\)

Tích phân trước bạn tự tính, tích phân sau cũng đơn giản thôi:

Đặt \(\left\{{}\begin{matrix}u=4x+13\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=4dx\\v=-e^{-x}\end{matrix}\right.\)

\(\Rightarrow I=-\left(4x+13\right).e^{-x}|^1_0+4\int\limits^1_0e^{-x}dx=\frac{-17}{e}+13-4.e^{-x}|^1_0=17-\frac{21}{e}\)

Casio cho kết quả tích phân trước là \(-\frac{97}{12}\)

Vậy \(\int\limits^1_0f\left(x\right)dx=\frac{107}{12}-\frac{21}{e}\)