Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(f'\left(x\right)=f'\left(1-x\right)\Rightarrow\int f'\left(x\right)dx=\int f'\left(1-x\right)dx\)
\(\Rightarrow f\left(x\right)=-f\left(1-x\right)+C\Rightarrow f\left(x\right)+f\left(1-x\right)=C\)
Thay \(x=0\Rightarrow f\left(0\right)+f\left(1\right)=C\Rightarrow C=42\)
\(\Rightarrow\int\limits^1_0\left[f\left(x\right)+f\left(1-x\right)\right]dx=\int\limits^1_042dx=42\)
Xét \(I=\int\limits^1_0f\left(1-x\right)dx\)
Đặt \(1-x=u\Rightarrow dx=-du;\left\{{}\begin{matrix}x=0\Rightarrow u=1\\x=1\Rightarrow u=0\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^0_1f\left(u\right).\left(-du\right)=\int\limits^1_0f\left(u\right).du=\int\limits^1_0f\left(x\right)dx\)
\(\Rightarrow2\int\limits^1_0f\left(x\right)dx=42\Rightarrow\int\limits^1_0f\left(x\right)dx=21\)

Đề là cho \(\int\limits^{\dfrac{\pi}{2}}_0sin2x.f\left(cos^2x\right)dx=1\)
Tính \(\int\limits^1_0\left[2f\left(1-x\right)-3x^2+5\right]dx\)
Đúng ko nhỉ?
Xét \(\int\limits^{\dfrac{\pi}{2}}_0sin2x.f\left(cos^2x\right)dx\)
Đặt \(cos^2x=1-u\Rightarrow-2sinx.cosxdx=-du\) \(\Rightarrow sin2xdx=du\)
\(\left\{{}\begin{matrix}x=0\Rightarrow u=0\\x=\dfrac{\pi}{2}\Rightarrow u=1\end{matrix}\right.\) \(\Rightarrow I=\int\limits^1_0f\left(1-u\right)du=\int\limits^1_0f\left(1-x\right)dx\)
\(\Rightarrow\int\limits^1_0f\left(1-x\right)dx=1\)
\(\Rightarrow\int\limits^1_0\left[2f\left(1-x\right)-3x^2+5\right]dx=2\int\limits^1_0f\left(1-x\right)dx-\int\limits^1_0\left(3x^2-5\right)dx\)
\(=2.1-\left(-4\right)=6\)

Chọn C.
Ta có f ' x + 2 f x = 0 ⇔ f ' x = - 2 f x ⇔ f ' x f x = - 2 d o f x > 0
Lấy tích phân hai vế, ta được
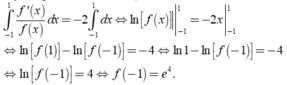

Chọn C.
Đặt u = G ( x ) d v = f ( x ) d x ⇒ d u = G ( x ) ' d x = g ( x ) d x v = ∫ f ( x ) d x = F ( x )
Suy ra: I = G ( x ) F ( x ) 2 0 - ∫ 0 2 F ( x ) g ( x ) d x
= G(2)F(2) – G(0)F(0) – 3 = 1 – 0 – 3 = -2.

\(I=\int\limits^{\frac{\pi}{3}}_{\frac{\pi}{6}}\frac{sin^2x.cosx+2sin2x}{\left(f\left(sinx\right)\right)^2}dx=\int\limits^{\frac{\pi}{3}}_{\frac{\pi}{6}}\frac{\left(sin^2x+4sinx\right).cosx}{\left(f\left(sinx\right)\right)^2}dx\)
Đặt \(sinx=t\Rightarrow cosx.dx=dt;\left\{{}\begin{matrix}x=\frac{\pi}{6}\Rightarrow t=\frac{1}{2}\\x=\frac{\pi}{3}\Rightarrow t=\frac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^{\frac{\sqrt{3}}{2}}_{\frac{1}{2}}\frac{\left(t^2+4t\right)}{f^2\left(t\right)}dt=\int\limits^{\frac{\sqrt{3}}{2}}_{\frac{1}{2}}\frac{\left(x^2+4x\right)}{f^2\left(x\right)}dx\)
Lại có:
\(x+x.f'\left(x\right)=2f\left(x\right)-4\Leftrightarrow x+4=2f\left(x\right)-x.f'\left(x\right)\)
\(\Leftrightarrow x^2+4x=2x.f\left(x\right)-x^2.f'\left(x\right)\)
\(\Leftrightarrow\frac{x^2+4x}{f^2\left(x\right)}=\frac{2x.f\left(x\right)-x^2.f'\left(x\right)}{f^2\left(x\right)}=\left(\frac{x^2}{f\left(x\right)}\right)'\)
\(\Rightarrow I=\int\limits^{\frac{\sqrt{3}}{2}}_{\frac{1}{2}}\left(\frac{x^2}{f\left(x\right)}\right)'dx=\frac{x^2}{f\left(x\right)}|^{\frac{\sqrt{3}}{2}}_{\frac{1}{2}}=\frac{\left(\frac{\sqrt{3}}{2}\right)^2}{f\left(\frac{\sqrt{3}}{2}\right)}-\frac{\left(\frac{1}{2}\right)^2}{f\left(\frac{1}{2}\right)}=\frac{3}{4b}-\frac{1}{4a}\)

Vẫn là đạo hàm của tích
Dễ dàng viết được:
\(\left[f'\left(x\right)\right]^2+f\left(x\right).f''\left(x\right)=\left[f\left(x\right)\right]'.f'\left(x\right)+f\left(x\right).\left[f'\left(x\right)\right]'=\left[f'\left(x\right).f\left(x\right)\right]'\)
Do đó giả thiết biến đổi thành:
\(\left[f'\left(x\right).f\left(x\right)\right]'=15x^4+12x\)
Nguyên hàm 2 vế:
\(f'\left(x\right).f\left(x\right)=\int\left(15x^4+12x\right)dx=3x^5+6x^2+C\)
Thay \(x=0\)
\(\Rightarrow f'\left(0\right).f\left(0\right)=C\Rightarrow C=1\)
\(\Rightarrow f'\left(x\right).f\left(x\right)=3x^5+6x^2+1\)
Tiếp tục nguyên hàm 2 vế:
\(\int f\left(x\right).f'\left(x\right)dx=\int\left(3x^5+6x^2+1\right)dx\) với chú ý \(\int f\left(x\right).f'\left(x\right)dx=\int f\left(x\right).d\left[f\left(x\right)\right]=\dfrac{1}{2}f^2\left(x\right)+C\)
Nên:
\(\Rightarrow\dfrac{1}{2}f^2\left(x\right)=\dfrac{1}{2}x^6+2x^3+x+C\)
Thay \(x=0\Rightarrow C=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{1}{2}f^2\left(x\right)=\dfrac{1}{2}x^6+2x^3+x+\dfrac{1}{2}\)
\(\Rightarrow f^2\left(1\right)\)
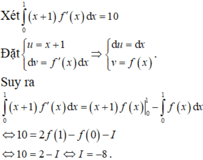
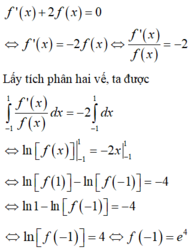
\(f\left(x\right)+2f'\left(x\right)+f''\left(x\right)=x^3+2x^2\)
\(\Leftrightarrow f\left(x\right)+f'\left(x\right)+f'\left(x\right)+f''\left(x\right)=x^3+2x^2\)
\(\Leftrightarrow f\left(x\right)+f'\left(x\right)+\left[f\left(x\right)+f'\left(x\right)\right]'=x^3+2x^2\)
Đặt \(f\left(x\right)+f'\left(x\right)=u\left(x\right)\) ta được:
\(u\left(x\right)+u'\left(x\right)=x^3+2x^2\)
\(\Leftrightarrow e^x.u\left(x\right)+e^x.u'\left(x\right)=e^x\left(x^3+2x^2\right)\)
\(\Leftrightarrow\left[e^x.u\left(x\right)\right]'=e^x\left(x^3+2x^2\right)\)
\(\Rightarrow e^x.u\left(x\right)=\int e^x\left(x^3+2x^2\right)dx=e^x\left(x^3-x^2+2x-2\right)+C\)
\(\Leftrightarrow e^x\left[f\left(x\right)+f'\left(x\right)\right]=e^x\left(x^3-x^2+2x-2\right)+C\)
Thay \(x=0\) vào ta được \(2=-2+C\Rightarrow C=4\)
\(\Rightarrow e^x.f\left(x\right)+e^x.f'\left(x\right)=e^x\left(x^3-x^2+2x-2\right)+4\)
\(\Leftrightarrow\left[e^x.f\left(x\right)\right]'=e^x\left(x^3-x^2+2x-2\right)+4\)
\(\Rightarrow e^x.f\left(x\right)=\int\left[e^x\left(x^3-x^2+2x-2\right)+4\right]dx\)
\(\Rightarrow e^x.f\left(x\right)=e^x\left(x^3-4x^2+10x-12\right)+4x+C_1\)
Thay \(x=0\) vào ta được: \(1=-12+C_1\Rightarrow C_1=13\)
\(\Rightarrow e^x.f\left(x\right)=e^x\left(x^3-4x^2+10x-12\right)+4x+13\)
\(\Rightarrow f\left(x\right)=x^3-4x^2+10x-12+\frac{4x+13}{e^x}\)
\(\Rightarrow\int\limits^1_0f\left(x\right)dx=\int\limits^1_0\left(x^3-4x^2+10x-12\right)dx+\int\limits^1_0\left(4x+13\right).e^{-x}dx\)
Tích phân trước bạn tự tính, tích phân sau cũng đơn giản thôi:
Đặt \(\left\{{}\begin{matrix}u=4x+13\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=4dx\\v=-e^{-x}\end{matrix}\right.\)
\(\Rightarrow I=-\left(4x+13\right).e^{-x}|^1_0+4\int\limits^1_0e^{-x}dx=\frac{-17}{e}+13-4.e^{-x}|^1_0=17-\frac{21}{e}\)
Casio cho kết quả tích phân trước là \(-\frac{97}{12}\)
Vậy \(\int\limits^1_0f\left(x\right)dx=\frac{107}{12}-\frac{21}{e}\)