Mọi người giúp mình bài này với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{24\cdot12}{24+12}=8\Omega\)
\(I=\dfrac{U}{R}=\dfrac{12}{8}=1,5A\)
\(P=\dfrac{U^2}{R}=\dfrac{12^2}{8}=18W\)
\(Q_{tỏa1}=A_1=U_1\cdot I_1\cdot t=12\cdot\dfrac{12}{24}\cdot1\cdot3600=21600J\)
\(Q_{tỏa2}=A_2=U_2\cdot I_2\cdot t=12\cdot\dfrac{12}{12}\cdot1\cdot3600=43200J\)

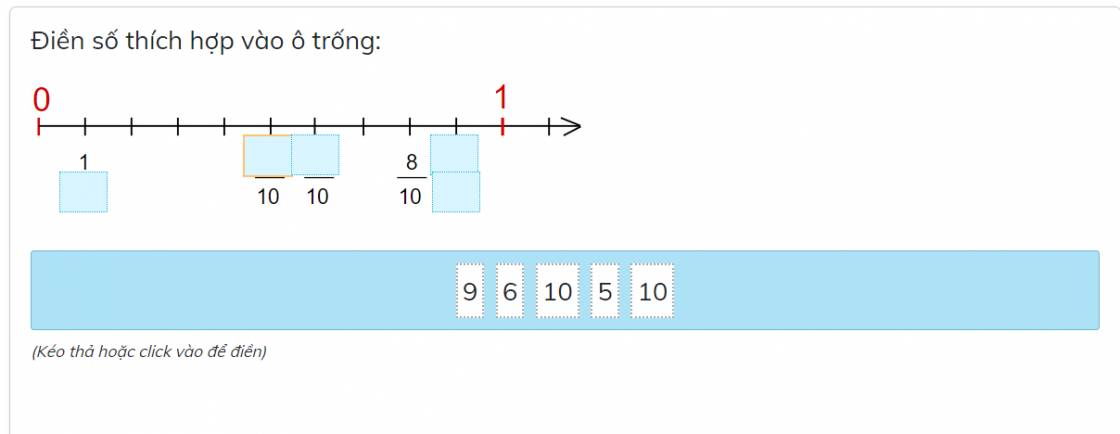
Từ 0 đến 1 được chia thành 10 phần bằng nhau.
Giá trị của mỗi phần là: \(\dfrac{1}{10}\)
Từ lập luận trên ta có:
Số thích hợp để điền vào các ô trống lần lượt là:
10; 5; 6; 9; 10
0 ; 1/10 ; 2/10 ; 3/10 ; 4/10 ; 5/10 ; 6/10 ; 7/10 ; 8/10 ; 9/10 ; 1
Chúc bạn học tốt!

Bài 2:
a) Để hàm số đồng biến thì m+1>0
hay m>-1
b) Để hàm số đi qua điểm A(2;4) thì
Thay x=2 và y=4 vào hàm số, ta được:
\(\left(m+1\right)\cdot2=4\)
\(\Leftrightarrow m+1=2\)
hay m=1
c) Để hàm số đi qua điểm B(2;-4) thì
Thay x=2 và y=-4 vào hàm số, ta được:
\(2\left(m+1\right)=-4\)
\(\Leftrightarrow m+1=-2\)
hay m=-3
Bài 1:
b) Ta có: \(5\cdot\sqrt{25a^2}-25a\)
\(=5\cdot5\cdot\left|a\right|-25a\)
\(=-25a-25a=-50a\)


1/
PT $\Leftrightarrow \sin ^2x-(1-\sin ^2x)+\sin x-2=0$
$\Leftrightarrow 2\sin ^2x+\sin x-3=0$
$\Leftrightarrow (\sin x-1)(2\sin x+3)=0$
$\Leftrightarrow \sin x=1$ (chọn) hoặc $\sin x=-\frac{3}{2}< -1$ (loại)
Vậy $\sin x=1$
$\Leftrightarrow x=\frac{\pi}{2}+2k\pi$ với $k$ nguyên.
4/
ĐKXĐ: $\tan x\neq -1$
PT $\Rightarrow \cos ^2x(\cos x-1)=2(\sin x+1)(\sin x+\cos x)$
$\Leftrightarrow (1-\sin ^2x)(\cos x-1)=2(\sin x+1)(\sin x+\cos x)$
$\Leftrightarrow (1-\sin x)(1+\sin x)(\cos x-1)=2(\sin x+1)(\sin x+\cos x)$
$\Leftrightarrow (\sin x+1)[(1-\sin x)(\cos x-1)-2(\sin x+\cos x)]=0$
$\Leftrightarrow (\sin x+1)(-1-\sin x\cos x-\sin x-\cos x)=0$
$\Leftrightarrow (\sin x+1)^2(\cos x+1)=0$
Nếu $\sin x=-1\Rightarrow x=\frac{-\pi}{2}+2k\pi$ với $k$ nguyên (tm)
Nếu $\cos x=-1\Rightarrow x=\pi +2k\pi$ với $k$ nguyên.


Mặt cầu tâm \(I\left(1;1;0\right)\) bán kính \(R=5\)
\(\Rightarrow IA=\sqrt{6^2+8^2}=10=2R\)
Gọi C là trung điểm IA \(\Rightarrow C\left(4;5;0\right)\Rightarrow IC=R=5\Rightarrow C\in\left(S\right)\)
Gọi D là trung điểm IC \(\Rightarrow D\left(\dfrac{5}{2};3;0\right)\), đồng thời do D là trung điểm IC \(\Rightarrow MD\perp IC\) và IM=IC=R hay tam giác MDF vuông tại D
Lại có: \(CM=CA=CI=R\Rightarrow\) tam giác AMI vuông tại M
\(\Rightarrow\Delta_VMID\sim\Delta_VAIM\) (chung góc I)
\(\Rightarrow\dfrac{MA}{MD}=\dfrac{AI}{AM}=\dfrac{2R}{R}=2\Rightarrow MA=2MD\)
\(\Rightarrow P=MA+2MB=2MD+2MB=2\left(MD+MB\right)\ge2DB=2\sqrt{\left(\dfrac{5}{2}\right)^2+\left(3-8\right)^2+0^2}=5\sqrt{5}\)




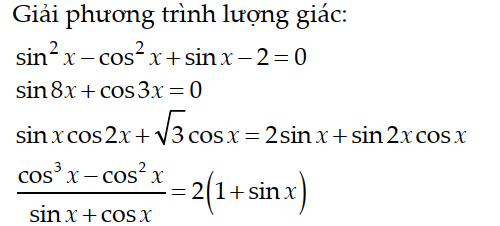



4: Ta có: \(\sqrt{3+2\sqrt{2}}+\sqrt{6-4\sqrt{2}}\)
\(=\sqrt{2}+1+2-\sqrt{2}\)
=3
5: Ta có: \(2+\sqrt{17-4\sqrt{9}+4\sqrt{5}}\)
\(=2+\sqrt{5+4\sqrt{5}}\)
6: Ta có: \(2\sqrt{3}+\sqrt{2}+\sqrt{18-8\sqrt{2}}\)
\(=2\sqrt{3}+\sqrt{2}+4-\sqrt{2}\)
\(=4+2\sqrt{3}\)