Giải phương trình: 2sin2x + 2cos4x = 2cos2x + sinx.cosx
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 3 2019
Hướng dẫn giải:
Chọn A.
không là nghiệm của phương trình
Chia 2 vế phương trình cho cos2x ta được
CM
3 tháng 9 2018
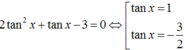
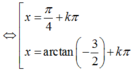
Đáp án C
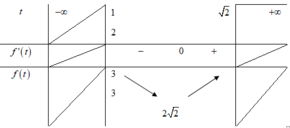
Mà phương trình f t = m ⇒ để phương trình có nghiệm thì m ∈ 2 2 ; 3 .
CM
21 tháng 4 2017
Đáp án C
Phương trình tương đương với:
Phương trình có nghiệm:
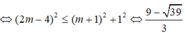
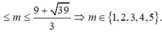
Có 5 số nguyên thoả mãn
16 tháng 8 2021
a) <=> 4sinxcosx -(2cos2x-1)=7sinx+2cosx-4
<=> 2cos2x+(2-4sinx)cosx+7sinx-5=0
- sinx=1 => 2cos2x-2cosx+2=0
pt trên vn
16 tháng 8 2021
b) <=> 2sinxcosx-1+2sin2x+3sinx-cosx-1=0
<=> cos(2sinx-1)+2sin2x+3sinx-2=0
<=> cosx(2sinx-1)+(2sinx-1)(sinx+2)=0
<=> (2sinx-1)(cosx+sinx+2)=0
<=> sinx=1/2 hoặc cosx+sinx=-2(vn)
<=> x= \(\frac{\pi}{6}+k2\pi\) hoặc \(x=\frac{5\pi}{6}+k2\pi\left(k\in Z\right)\)
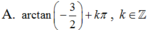
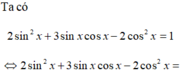
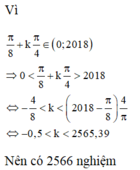
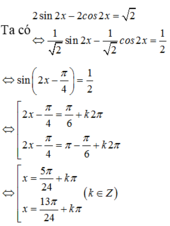
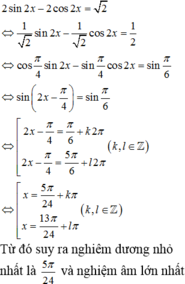
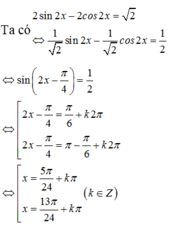
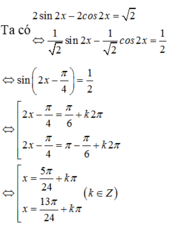
ta có : \(2sin^2x+2cos^4x=2cos^2x+sinx.cosx\)
\(\Leftrightarrow2sin^2x+2cos^2x\left(cos^2x-1\right)-sinx.cosx=0\)
\(\Leftrightarrow2sin^2x-2cos^2x.sin^2x-sinx.cosx=0\)
\(\Leftrightarrow2sin^2x\left(1-cos^2x\right)-sinx.cosx=0\)
\(\Leftrightarrow2sin^4x-sinx.cosx=sinx\left(2sin^3x-cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\2sin^3x-cosx=0\end{matrix}\right.\)
tới đây bn giải như phương trình dạng bình thường nha :)