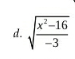(tìm điều kiện xác định)
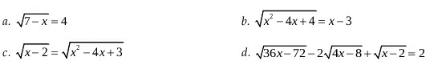( tìm x biết)
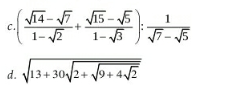(rút gọn)
Các anh e giúp mik vs
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 8 2021
a: ĐKXĐ: \(x>0\)
b: Ta có: \(A=\dfrac{x^2+\sqrt{x}}{x-\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+1\)
\(=x+\sqrt{x}-2\sqrt{x}-1+1\)
\(=x-\sqrt{x}\)
Y
6 tháng 4 2023
\(M=\dfrac{4}{x+2}+\dfrac{3}{x-2}-\dfrac{5x+2}{x^2-4}\left(dkxd:x\ne\pm2\right)\)
\(=\dfrac{4}{x+2}+\dfrac{3}{x-2}-\dfrac{5x+2}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{4\left(x-2\right)+3\left(x+2\right)-\left(5x+2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{4x-8+3x+6-5x-2}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x-4}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2}{x+2}\)
Để \(M=\dfrac{2}{5}\) thì \(\dfrac{2}{x+2}=\dfrac{2}{5}\)
Suy ra :
\(2.5=2\left(x+2\right)\)
\(\Leftrightarrow2x+4=10\)
\(\Leftrightarrow x=3\)
Vậy \(M=\dfrac{2}{5}\) thì x = 3
PT
1
10 tháng 11 2021
\(a,ĐK:x\ne\pm1;x\ne0\\ M=\dfrac{1-x+2x}{\left(1+x\right)\left(1-x\right)}:\dfrac{1-x}{x}\\ M=\dfrac{x+1}{\left(x+1\right)\left(1-x\right)}\cdot\dfrac{x}{1-x}=\dfrac{x}{\left(1-x\right)^2}\\ b,ĐK:x\ge0;x\ne4\\ N=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ N=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)
Tất cả đều phải tìm điều kiện
tìm điều kiện xác định và rút gọn ạaaa
25 tháng 11 2023
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x-2\sqrt{x}< >0\\\sqrt{x}-2< >0\\x-4\sqrt{x}+4< >0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=0\\x< >4\\\left(\sqrt{x}-2\right)^2< >0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=0\\x< >4\end{matrix}\right.\)
T
1
25 tháng 2 2023
b: ĐKXD: x<>1/5; x<>3
PT\(\Leftrightarrow\dfrac{3}{5x-1}-\dfrac{2}{x-3}=\dfrac{-4}{\left(5x-1\right)\left(x-3\right)}\)
=>3x-9-10x+2=-4
=>-7x-7=-4
=>-7x=3
=>x=-3/7
a: ĐKXĐ: x<>2/3; x<>-2/3
\(PT\Leftrightarrow\left(3x+2\right)^2-6\left(3x-2\right)=9x\)
=>9x^2+12x+4-18x+12-9x=0
=>9x^2-15x+16=0
=>\(x\in\varnothing\)
c: ĐKXĐ: x<>1/4; x<>-1/4
PT =>-3(4x+1)=2(4x-1)-6x-8
=>-12x-3=8x-2-6x-8
=>-12x-3=2x-10
=>-14x=-7
=>x=1/2
d: ĐKXĐ: x<>0; x<>2
\(\Leftrightarrow\dfrac{5-x}{4x\left(x-2\right)}+\dfrac{7}{8x}=\dfrac{x-1}{2x\left(x-2\right)}+\dfrac{1}{8\left(x-2\right)}\)
=>2(5-x)+7(x-2)=4(x-1)+x
=>10-2x+7x-14=4x-4+x
=>5x-4=5x-4
=>0x=0(luôn đung)
Vậy: S=R\{0;2}
e: DKXĐ: x<>0
PT \(\Leftrightarrow\dfrac{\left(x+1\right)\left(x^2-x+1\right)-\left(x-1\right)\left(x^2+x+1\right)}{\left(x^2+x+1\right)\left(x^2-x+1\right)}=\dfrac{3}{x\left(x^2+x+1\right)\left(x^2-x+1\right)}\)
=>x(x^3+1-x^3+1)=3
=>2x=3
=>x=3/2
sau mỗi ý đều có đầu bài nha
ĐKXĐ: \(\dfrac{x^2-16}{-3}\ge0\)
vì \(-3< 0\) nên \(x^2-16\le0\Rightarrow x^2\le16\Rightarrow-4\le x\le4\)