7) Cho hàm số y=\(\left(3-\sqrt{2}\right)x+1\). Tính giá trị của x khi y nhận các giá trị sau: 0; 1; 8; \(2+\sqrt{2}\) ; \(2-\sqrt{2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
11 tháng 9 2023
a) \(f\left( 1 \right) = 3.1 = 3;f\left( { - 2} \right) = 3.\left( { - 2} \right) = - 6;f\left( {\dfrac{1}{3}} \right) = 3.\dfrac{1}{3} = 1\).
b) Ta có: \(f\left( { - 3} \right) = 3.\left( { - 3} \right) = - 9;f\left( { - 1} \right) = 3.\left( { - 1} \right) = - 3\)
\(f\left( 0 \right) = 3.0 = 0;f\left( 2 \right) = 3.2 = 6;f\left( 3 \right) = 3.3 = 9\);
Ta lập được bảng sau
\(x\) | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
\(y\) | –9 | -6 | –3 | 0 | 3 | 6 | 9 |
CM
9 tháng 3 2017
Các giá trị của y được thể hiện trong bảng sau:
| x | 0 | 1 | 2 | 3 + 2 | 3 - 2 |
| y = (3 - 2 )x + 1 | 1 | 4 - 2 | 3 2 - 1 | 8 | 12 - 6 2 |
22 tháng 7 2021
a) Vì \(3-2\sqrt{2}>0\) nên hàm số đồng biến
b) Thay \(x=3+2\sqrt{2}\) vào hàm số, ta được:
\(y=\left(3-2\sqrt{2}\right)\left(3+2\sqrt{2}\right)+\sqrt{2}-1\)
\(=9-8+\sqrt{2}-1\)
\(=\sqrt{2}\)
TA
22 tháng 7 2021
a) `a=3-2\sqrt2>0 =>` Hàm số đồng biến.
b) `y=(3-2\sqrt2)(3+2\sqrt2)+\sqrt2-1=3^2-(2\sqrt2)^2+\sqrt2-1=\sqrt2`
`=> y=\sqrt2` khi `x=3+2\sqrt2`
24 tháng 10 2021
a, Vì \(5-3\sqrt{2}>0\) nên hs đồng biến trên R
b, \(x=5+3\sqrt{2}\Leftrightarrow y=25-18+\sqrt{2}-1=6+\sqrt{2}\)
c, \(y=0\Leftrightarrow\left(5-3\sqrt{2}\right)x+\sqrt{2}-1=0\Leftrightarrow x=\dfrac{1-\sqrt{2}}{5-3\sqrt{2}}\)
\(\Leftrightarrow x=\dfrac{\left(1-\sqrt{2}\right)\left(5+3\sqrt{2}\right)}{7}=\dfrac{-2\sqrt{2}-1}{7}\)
AH
Akai Haruma
Giáo viên
12 tháng 9 2021
Lời giải:
a. Vì $\sqrt{3}-1>0$ nên hàm trên là hàm đồng biến trên $\mathbb{R}$
b.
$F(0)=(\sqrt{3}-1).0+1=1$
$F(\sqrt{3}+1)=(\sqrt{3}-1)(\sqrt{3}+1)+1=(3-1)+1=3$
5 tháng 2 2022
a: Để y>0 thì x-7<0
hay x<7
b: Để y<0 thì x-7>0
hay x>7
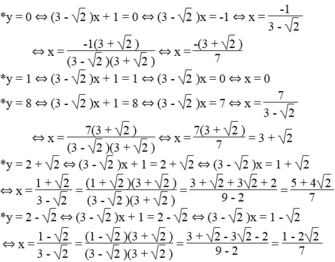
Thay y=0 vào hàm số, ta được:
\(\left(3-\sqrt{2}\right)x+1=0\)
\(\Leftrightarrow x=\dfrac{-3-\sqrt{2}}{7}\)