Giải tự luận giúp em 1209 hoặc cả 2 câu thì càng tốt ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2: FK vuôg góc BE; AE vuông góc BE
=>FK//AE
Chứng minh tương tự, ta được AF//EK
=>AFKE là hbh
=>AF=EK
=>AF/EC=EK/EC
ΔCEK đồng dạng với ΔCAM
=>EK/EC=AM/AC
=>AF/EC=AM/AC
ΔAFB đồng dạng với ΔCEB
=>góc ABF=góc CBE
c: AM/AC=AF/EC=AB/BC
=>AM/AC=AB/BC
=>ΔAMB đồng dạng với ΔCAB
=>góc ABC=góc ABM
=>BA là phân giác của góc MBC


a: \(=\dfrac{-\dfrac{1}{2}\left[cos\left(a+b+a-b\right)-cos\left(a+b-a+b\right)\right]}{cos^2b-cos^2a}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left[cos2a-cos2b\right]}{\dfrac{1-cos2b}{2}-\dfrac{1-cos2a}{2}}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1-cos2b-1+cos2a}{2}}=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}=-1\)
c: \(T=\dfrac{sina+sinb\cdot\left(cosa\cdot cosb-sina\cdot sinb\right)}{cosa-sinb\cdot\left(sina\cdot cosb+sinb\cdot cosa\right)}-tan\left(a+b\right)\)
\(=\dfrac{sina+sinb\cdot cosa\cdot cosb-sin^2b\cdot sina}{cosa-sinb\cdot sina\cdot cosb-sin^2b\cdot cosa}-tan\left(a+b\right)\)
\(=\dfrac{sina\left(1-sin^2b\right)+sinb\cdot cosa\cdot cosb}{cosa\left(1-sin^2b\right)-sinb\cdot sina\cdot cosb}\)-tan(a+b)
\(=\dfrac{sina\cdot cos^2b+sinb\cdot cosa\cdot cosb}{cosa\cdot cos^2b-sinb\cdot sina\cdot cosb}-tan\left(a+b\right)\)
\(=\dfrac{sina\cdot cosb+sinb\cdot cosa}{cosa\cdot cosb-sina\cdot sinb}-tan\left(a+b\right)\)
\(=\dfrac{sin\left(a+b\right)}{cos\left(a+b\right)}-tan\left(a+b\right)=0\)

\(A=\dfrac{2^{13}\cdot3^7}{2^{15}\cdot3^2\cdot9^2}=\dfrac{2^{13}\cdot3^7}{2^{15}\cdot3^6}=\dfrac{3}{4}\)
\(C=27\cdot\left(-\dfrac{3}{2}\right)^{-5}\cdot\left(-\dfrac{2}{5}\right)^{-4}:\left(\dfrac{2}{125}\right)^{-1}\)
\(=27\cdot\dfrac{-32}{243}\cdot\dfrac{625}{16}\cdot\dfrac{2}{125}\)
\(=\dfrac{-32}{9}\cdot\dfrac{1}{8}\cdot5\)
\(=-\dfrac{20}{9}\)

4.
\(\lim\limits_{x\rightarrow8}f\left(x\right)=\lim\limits_{x\rightarrow8}\dfrac{\sqrt[3]{x}-2}{x-8}=\lim\limits_{x\rightarrow8}\dfrac{x-8}{\left(x-8\right)\left(\sqrt[3]{x^2}+2\sqrt[3]{x}+4\right)}=\lim\limits_{x\rightarrow8}\dfrac{1}{\sqrt[3]{x^2}+2\sqrt[3]{x}+4}\)
\(=\dfrac{1}{4+4+4}=\dfrac{1}{12}\)
\(f\left(8\right)=3.8-20=4\)
\(\Rightarrow\lim\limits_{x\rightarrow8}f\left(x\right)\ne f\left(8\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=8\)
5.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{1+2x}-1+1-\sqrt[3]{1+3x}}{x}=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{2x}{\sqrt[]{1+2x}+1}-\dfrac{3x}{1+\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}}{x}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{2}{\sqrt[]{1+2x}+1}-\dfrac{3}{1+\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}\right)=\dfrac{2}{1+1}-\dfrac{3}{1+1+1}=0\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(3x^2-2x\right)=0\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=f\left(0\right)\)
\(\Rightarrow\) Hàm liên tục tại \(x=0\)
6.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{4x+1}-\sqrt[3]{6x+1}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{4x+1}-\left(2x+1\right)+\left(2x+1-\sqrt[3]{6x+1}\right)}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{-x^2}{\sqrt[]{4x+1}+2x+1}+\dfrac{x^2\left(8x+12\right)}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{-1}{\sqrt[]{4x+1}+2x+1}+\dfrac{8x+12}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}\right)\)
\(=\dfrac{-1}{1+1}+\dfrac{12}{1+1+1}=\dfrac{7}{2}\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(2-3x\right)=2\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)\ne\lim\limits_{x\rightarrow0^-}f\left(x\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=0\)

Bài 1:
a, \(\dfrac{2}{3}\) + \(\dfrac{1}{5}\). \(\dfrac{10}{7}\)
= \(\dfrac{2}{3}\) + \(\dfrac{2}{7}\)
= \(\dfrac{20}{21}\)
b, \(\dfrac{7}{12}\) - \(\dfrac{27}{7}\). \(\dfrac{1}{18}\)
= \(\dfrac{7}{12}\) - \(\dfrac{3}{14}\)
= \(\dfrac{31}{84}\)
c, \(\dfrac{3}{10}\). \(\dfrac{-5}{6}\) - \(\dfrac{1}{8}\)
= - \(\dfrac{1}{4}\) - \(\dfrac{1}{8}\)
= - \(\dfrac{3}{8}\)
d, - \(\dfrac{4}{9}\): \(\dfrac{8}{3}\) + \(\dfrac{1}{18}\)
= - \(\dfrac{1}{6}\) + \(\dfrac{1}{18}\)
= - \(\dfrac{1}{9}\)
e, {[(\(\dfrac{1}{2}\) - \(\dfrac{2}{3}\))2 : 2 ] - 1}. \(\dfrac{4}{5}\)
= {[ (-\(\dfrac{1}{6}\))2 : 2] - 1}. \(\dfrac{4}{5}\)
= { [\(\dfrac{1}{36}\) : 2] - 1}. \(\dfrac{4}{5}\)
= { \(\dfrac{1}{72}\) - 1}. \(\dfrac{4}{5}\)
=- \(\dfrac{71}{72}\).\(\dfrac{4}{5}\)
= -\(\dfrac{71}{90}\)

 ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn
ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn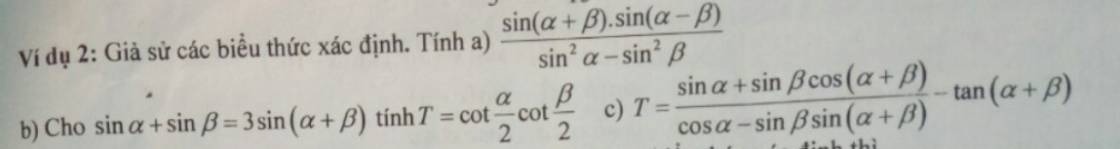
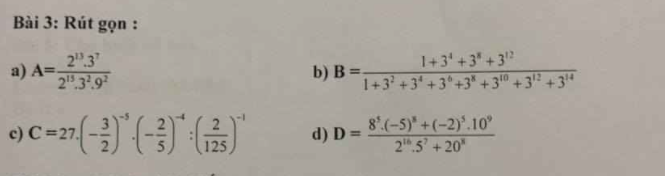 giúp mình với ạ cả 4 câu càng nhanh càng tốt
giúp mình với ạ cả 4 câu càng nhanh càng tốt

Cách làm nói chung:
- Tìm vecto chỉ phương \(\overrightarrow{u}\) của đường d và vtpt \(\overrightarrow{n}\) của mặt (P)
- Tính tích có hướng \(\overrightarrow{u_1}=\left(\overrightarrow{u};\overrightarrow{n}\right)\)
- Tiếp tục tính tích có hướng \(\overrightarrow{u_2}=\left[\overrightarrow{u_1};\overrightarrow{n}\right]\)
- Tìm tọa độ giao điểm M của d và (P)
- Hình chiếu vuông góc của d lên (P) sẽ đi qua M và nhận \(\overrightarrow{u_2}\) (hoặc 1 vecto cùng phương với nó) là 1 vtcp
Lưu ý rằng có vô số cách viết 1 pt đường thẳng (tùy thuộc cách chọn điểm) nên có thể trong 4 đáp án của đề bài không đáp án nào giống pt vừa viết được. Lúc đó cần kiểm tra bằng cách: 1. Loại những đáp án không giống vecto chỉ phương. 2. Trong những đáp án còn lại, tìm 1 điểm trên đó và thay vào pt đường thẳng vừa viết được, nếu thỏa mãn thì đó là đáp án đúng.
1209.
d nhận \(\overrightarrow{u}=\left(1;1;-1\right)\) là 1 vtcp
(P) nhận \(\overrightarrow{n}=\left(1;2;1\right)\) là 1 vtpt
Ta có: \(\overrightarrow{u_1}=\left[\overrightarrow{u};\overrightarrow{n}\right]=\left(3;-2;1\right)\)
\(\overrightarrow{u_2}=\left[\overrightarrow{u_1};\overrightarrow{n}\right]=\left(-4;-2;8\right)=-2\left(2;1;-4\right)\)
Phương trình d dạng tham số: \(\left\{{}\begin{matrix}x=t\\y=1+t\\z=2-t\end{matrix}\right.\)
Gọi M là giao điểm d và (P), tọa độ M thỏa mãn:
\(t+2\left(1+t\right)+2-t-4=0\Rightarrow t=0\Rightarrow M\left(0;1;2\right)\)
Do đó hình chiếu của d lên (P) nhận (2;1;-4) là 1 vtcp và đi qua M(0;1;2)
Phương trình: \(\dfrac{x}{2}=\dfrac{y-1}{1}=\dfrac{z-2}{-4}\)
Câu 1210 hoàn toàn tương tự