Giúp mình làm chi tiết với

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tham khảo
vi phạm phương châm quan hệ.
vì sử dụng từ đồng âm khác nghĩa làm sai ý ngườ hỏi
a) Họp xong bạn nhớ đi ra cửa trước
- Phương châm hội thoại vi phạm: phương châm về lượng ( nội dung cần truyền đạt chưa cụ thể, rõ ràng )
- Sửa lại:
Họp xong bạn nhớ đi ra cửa trước
⇒ Họp xong bạn nhớ đi ra cửa trước của tòa nhà A tầng 1 nhé

b: ΔOAH cân tại O(Do A,H cùng nằm trên (O))
mà OD là đường cao
nên OD là phân giác của góc AOH
Xét ΔOAD và ΔOHD có
OA=OH
góc AOD=góc HOD
OD chung
Do đó: ΔOAD=ΔOHD
=>góc OHD=góc OAD=90 độ
=>DH vuông góc OH

a)PQ \(\left\{{}\begin{matrix}quaP\left(1;-4\right)\\vtcp\overrightarrow{PQ}\left(1;7\right)\Rightarrow vtpt\overrightarrow{n}\left(7;-1\right)\end{matrix}\right.\)
\(\Rightarrow PQ:7x-y-11=0\)
b) Gọi pt đt tâm (O) có dạng (C):\(x^2+y^2=R^2\)
Do (C) tiếp xúc với đt \(2x+y-3=0\)
\(\Rightarrow R=d_{\left(O;\Delta\right)}=\dfrac{\left|2.0+0-3\right|}{\sqrt{2^2+1}}=\dfrac{3\sqrt{5}}{5}\)
\(\Rightarrow\left(C\right):x^2+y^2=\dfrac{9}{5}\)
c)\(I\in\left(\Delta\right)\Rightarrow I\left(t;3-2t\right)\)
\(IQ=R\Leftrightarrow\sqrt{\left(2-t\right)^2+4t^2}=3\)
\(\Rightarrow\left[{}\begin{matrix}t=\dfrac{2+\sqrt{29}}{5}\\t=\dfrac{2-\sqrt{29}}{5}\end{matrix}\right.\)\(\Rightarrow I\left(\dfrac{2+\sqrt{29}}{5};\dfrac{11-2\sqrt{29}}{5}\right);I\left(\dfrac{2-\sqrt{29}}{5};\dfrac{11+2\sqrt{29}}{5}\right)\)
Vậy pt đường tròn tâm I cần tìm là: \(\left(C\right)':\left(x-\dfrac{2+\sqrt{29}}{5}\right)^2+\left(y-\dfrac{11-2\sqrt{29}}{5}\right)^2=9\) hoặc \(\left(C\right)':\left(x-\dfrac{2-\sqrt{29}}{5}\right)^2+\left(y-\dfrac{11+2\sqrt{29}}{5}\right)^2=9\)
a.
\(\overrightarrow{PQ}=\left(1;7\right)\Rightarrow\) đường thẳng PQ nhận \(\left(7;-1\right)\) là 1 vtpt
Phương trình PQ:
\(7\left(x-2\right)-1\left(y-3\right)=0\Leftrightarrow7x-y-11=0\)
b.
Do đường tròn tiếp xúc denta nên \(R=d\left(O;\Delta\right)\)
\(\Rightarrow R=\dfrac{\left|2.0-0-3\right|}{\sqrt{2^2+1^2}}=\dfrac{3}{\sqrt{5}}\)
Phương trình đường tròn: \(x^2+y^2=\dfrac{9}{5}\)
c.
Do I thuộc denta nên tọa độ có dạng: \(I\left(a;3-2a\right)\)
\(\Rightarrow\overrightarrow{IQ}=\left(2-a;2a\right)\) \(\Rightarrow IQ^2=\left(2-a\right)^2+4a^2\)
Do đường tròn qua Q nên \(IQ=R\Rightarrow IQ^2=R^2\)
\(\Rightarrow\left(2-a\right)^2+4a^2=9\)
\(\Rightarrow5a^2-4a-5=0\Rightarrow\left[{}\begin{matrix}a=\dfrac{2+\sqrt{29}}{5}\\a=\dfrac{2-\sqrt{29}}{5}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}I\left(\dfrac{2+\sqrt{29}}{5};\dfrac{11-2\sqrt{29}}{5}\right)\\I\left(\dfrac{2-\sqrt{29}}{5};\dfrac{11+2\sqrt{29}}{5}\right)\end{matrix}\right.\)
Có 2 đường tròn thỏa mãn:
\(\left(x-\dfrac{2+\sqrt{29}}{5}\right)^2+\left(y-\dfrac{11-2\sqrt{29}}{5}\right)^2=9\)
\(\left(x-\dfrac{2-\sqrt{29}}{5}\right)^2+\left(y-\dfrac{11+2\sqrt{29}}{5}\right)^2=9\)

a:\(\dfrac{33}{44}=\dfrac{3}{4}\\ MSC:8\\ \dfrac{3}{4}=\dfrac{3\times2}{4\times2}=\dfrac{6}{8};\dfrac{2}{8}\)
b:\(\dfrac{9}{12}=\dfrac{3}{4};\dfrac{24}{36}=\dfrac{7}{9}\\ MSC:72\\ \dfrac{3}{4}=\dfrac{3\times18}{4\times18}=\dfrac{54}{72};\dfrac{7}{9}=\dfrac{7\times8}{9\times8}=\dfrac{56}{72};\dfrac{3}{8}=\dfrac{3\times9}{8\times9}=\dfrac{27}{72}\)

1 ko bt
2.các tác hại khi dùng internet là
+thông tin cá nhân bị lộ hoặc đánh cắp
+máy tính bi nhiễm virus hay mã độc
+lừa đảo,dụ dỗ,bắt nạt trên internet
+Tiếp cận thông tin ko chính xác
+Nghiện trò chơi trên mạng.
b. giữa an toàn thông tin,ko gặp gỡ người mà mk ko quen biết,chỉ đọc và mở thư điện tử và tin nhắn của người mk quen biết,tin cậy,nói ra với người bn tin tưởng
3.thuật toán là một dãy các chỉ dẫn rõ ràng sao co khi thực hiện những chỉ dẫn này người ta phải giải quyết đc vấn đề hoặc nhiệm vụ đã cho.ý thứ 2 ko vẽ đc sorry
4.cài đặt và cập nhập phần mềm trống virus
Cài đặt mật khuẩu mạnh
Tránh dùng mạng công cộng
..v..v
5.😅😥

Câu 1
Mỗi đất nước , mỗi quốc gia đều có đồng tiền riêng , nên nếu đổi được thì dễ dàng khi sang nước bạn
Nếu sang bên nước mà học bắt phải đổi tiền thì chúng ta sẽ bị áp thêm cái thuế đổi tiền đắt hơn nên cũng hơi bất tiện khi một đất nước dùng 2 loại đồng tiền nhỉ?
Câu 2
Chúng ta phải kiên quyết đấu tranh về tư tưởng và phong cách sống , giúp họ hiểu ra mặt tốt của nhà nước , nhưỡng cổ hủ , lạc hậu cần phải loại bỏ .
Là học sinh/ sinh viên em sẽ cố gắng rèn luyện , trao dồi kiến thức của đảng và nhà nước , vượt qua thử thách để thực hiện mục tiêu lí tưởng mà đã chọn

29. a)Mức độ sử dụng , và số lượng của các loại bia được sử dụng trong tết
b) Em sẽ dựa vào đó để điều chỉnh chất lượng , giá thành , nhân công , đầu mối cho hợp lí và có tỉ lệ thu lợi nhuận cao nhất
30
Nước ta đi theo hình thức xã hội chủ nghĩa đó là quá độ xã hội chủ nghĩa
Chúng ta đã bỏ qua XHTB , đó là bước nhảy cóc trong chính trị và chúng ta không vì hế từ bỏ lên một một giới hạn của một nước cuối cùng đó là độc lập , tự do , bình đẳng , bác ái .

Bài 2:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5$ (cm)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{3.4}{5}=2,4$ (cm)
Áp dụng định lý Pitago:
$BH=\sqrt{AB^2-AH^2}=\sqrt{3^2-2,4^2}=1,8$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{4^2-2,4^2}=3,2$ (cm)
b.
Áp dụng hệ thức lượng trong tam giác vuông:
$AH^2=BH.CH=9.16$
$\Rightarrow AH=12$ (cm)
Áp dụng định lý Pitago:
$AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+9^2}=15$ (cm)
$AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20$ (cm)
$BC=BH+CH=9+16=25$ (cm)
Bài 3:
Vì $AB:AC=3:4$ nên đặt $AB=3a; AC=4a$ (cm)
Áp dụng định lý Pitago:
$15=BC=\sqrt{AB^2+AC^2}=\sqrt{(3a)^2+(4a)^2}=5a$
$\Rightarrow a=3$ (cm)
$AH=\frac{AB.AC}{BC}=\frac{3a.4a}{5a}=2,4a$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{(3a)^2-(2,4a)^2}=1,8a=1,8.3=5,4$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{(4a)^2-(2,4a)^2}=3,2a=3,2.3=9,6$ (cm)



 Làm chi tiết từng câu ra giúp mình với ạ
Làm chi tiết từng câu ra giúp mình với ạ


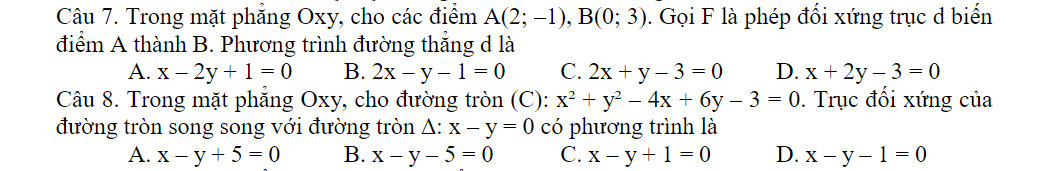 Làm giúp mình 2 bài này với, có giải chi tiết. Mình cảm ơn nhiều
Làm giúp mình 2 bài này với, có giải chi tiết. Mình cảm ơn nhiều
Câu 17: Ý A
\(\Delta:2x+3y-2=0\)
Kẻ đt d vuông góc với \(\Delta\) và đi qua M => Đường thẳng d có dạng: \(d:-3x+2y+c=0\)
\(M\in\left(d\right)\Rightarrow-3.3+2.3+c=0\Leftrightarrow c=3\)
\(\Rightarrow d:-3x+2y+3=0\)
Tọa độ hình chiếu vuông góc của M lên đt \(\Delta\) là nghiệm của hệ: \(\left\{{}\begin{matrix}2x+3y-2=0\\-3x+2y+3=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\)
Câu 18: B
Hàm có TXĐ là R khi \(x^2-2mx-2m+3\ge0;\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1>0\left(lđ\right)\\\Delta\le0\end{matrix}\right.\)\(\Rightarrow4m^2-4\left(-2m+3\right)\le0\)\(\Leftrightarrow-3\le m\le1\)
Có 5 giá trị nguyên của m
Câu 19: A
Bpt vô nghiệm khi \(x^2-mx+1>0;\forall x\)
\(\Leftrightarrow\Delta< 0\Leftrightarrow m^2-4< 0\Leftrightarrow-2< m< 2\)
Câu 20: D
\(D\in\Delta\Rightarrow D\left(t;-3t-2\right)\)
\(\Rightarrow\overrightarrow{AD}\left(t+1;-3t-2\right)\)
\(\overrightarrow{BC}\left(2;-1\right)\)
Vì ABCD là hình thang có một đáy là AD
\(\Rightarrow\)\(AD//BC\)
\(\Rightarrow\overrightarrow{AD}\) và \(\overrightarrow{BC}\) cùng phương
\(\Leftrightarrow\left(t+1\right)\left(-1\right)=2\left(-3t-2\right)\)\(\Leftrightarrow t=-\dfrac{3}{5}\)\(\Rightarrow D\left(-\dfrac{3}{5};\dfrac{-1}{5}\right)\)