
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vd1:
d) Ta có: \(\sqrt{2}\left(x-1\right)-\sqrt{50}=0\)
\(\Leftrightarrow\sqrt{2}\left(x-1-5\right)=0\)
\(\Leftrightarrow x=6\)

\(4,\\ 2.B=\sqrt{x}-1+\dfrac{2-2\sqrt{x}}{\sqrt{x}}\left(x>0\right)\\ B=\dfrac{x-\sqrt{x}+2-2\sqrt{x}}{\sqrt{x}}=\dfrac{x-3\sqrt{x}+2}{\sqrt{x}}\)
\(3.x=\sqrt{11+6\sqrt{2}}+\sqrt{11-6\sqrt{2}}=\left(3+\sqrt{2}\right)+\left(3-\sqrt{2}\right)=6\)
Thay vào B, ta được \(B=\dfrac{6-3\sqrt{6}+2}{\sqrt{6}}=\dfrac{6\sqrt{6}-18+2\sqrt{6}}{6}=\dfrac{4\sqrt{6}-9}{3}\)
\(4.B=0\Leftrightarrow\dfrac{x-3\sqrt{x}+2}{\sqrt{x}}=0\Leftrightarrow x-3\sqrt{x}+2=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=1\\\sqrt{x}=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=4\left(tm\right)\end{matrix}\right.\)
\(7.B\in Z\Leftrightarrow\dfrac{x-3\sqrt{x}+2}{\sqrt{x}}\in Z\Leftrightarrow\sqrt{x}-3+\dfrac{2}{\sqrt{x}}\in Z\\ \Leftrightarrow\dfrac{2}{\sqrt{x}}\in Z\Leftrightarrow\sqrt{x}\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\\ \Leftrightarrow x\in\left\{1;4\right\}\left(\sqrt{x}>0\right)\)

\(\Leftrightarrow n^5+n^2-n^2+1⋮n^3+1\)
\(\Leftrightarrow-n^3+n⋮n^3+1\)
\(\Leftrightarrow n=1\)

2\(\sqrt{\dfrac{16}{3}}\) - 3\(\sqrt{\dfrac{1}{27}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{3}{3\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{1}{\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{16}{2\sqrt{3}}\) - \(\dfrac{2}{2\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{11}{2\sqrt{3}}\)
= \(\dfrac{11\sqrt{3}}{6}\)
f, 2\(\sqrt{\dfrac{1}{2}}\)- \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{2}{\sqrt{2}}\) - \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5\sqrt{2}}{4}\)
(1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1- \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3+\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{3-1}\)
= \(\dfrac{-4}{2}\)
= -2

a) Ta có: \(\sqrt{\dfrac{a}{b}}+\sqrt{ab}+\dfrac{a}{b}\cdot\sqrt{\dfrac{b}{a}}\)
\(=\dfrac{\sqrt{ab}}{b}+\sqrt{ab}+\dfrac{a}{b}\cdot\dfrac{\sqrt{b}}{\sqrt{a}}\)
\(=\dfrac{\sqrt{ab}}{b}+\dfrac{b\sqrt{ab}}{b}+\dfrac{\sqrt{ab}}{b}\)
\(=\dfrac{b\sqrt{ab}+2\sqrt{ab}}{b}\)
b) \(\sqrt{\dfrac{m}{x^2-2x+1}}\cdot\sqrt{\dfrac{4mx^2-8mx+4m}{81}}\)
\(=\sqrt{\dfrac{m}{\left(x-1\right)^2}\cdot\dfrac{4m\left(x-1\right)^2}{81}}\)
\(=\sqrt{\dfrac{4m^2}{81}}=\dfrac{2m}{9}\)

Bạn nên tách lẻ các bài ra post riêng. Đăng thế này chiếm diện tích, khó quan sát => mọi người dễ bỏ qua bài của bạn.

a) Ta có: \(\dfrac{1}{2}\sqrt{48}-2\sqrt{75}-\dfrac{\sqrt{33}}{\sqrt{11}}+5\sqrt{1\dfrac{1}{3}}\)
\(=\dfrac{1}{2}\cdot4\sqrt{3}-2\cdot5\sqrt{3}-\sqrt{3}+5\cdot\dfrac{2}{\sqrt{3}}\)
\(=-9\sqrt{3}+\dfrac{10}{\sqrt{3}}\)
\(=\dfrac{-27+10}{\sqrt{3}}=\dfrac{-17\sqrt{3}}{3}\)

2: Thay x=1 và y=-4 vào (d), ta được:
2m+2=-4
hay m=-3

2:
1+cot^2a=1/sin^2a
=>1/sin^2a=1681/81
=>sin^2a=81/1681
=>sin a=9/41
=>cosa=40/41
tan a=1:40/9=9/40



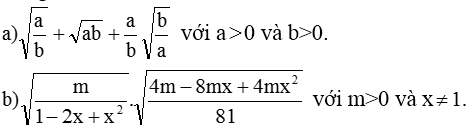
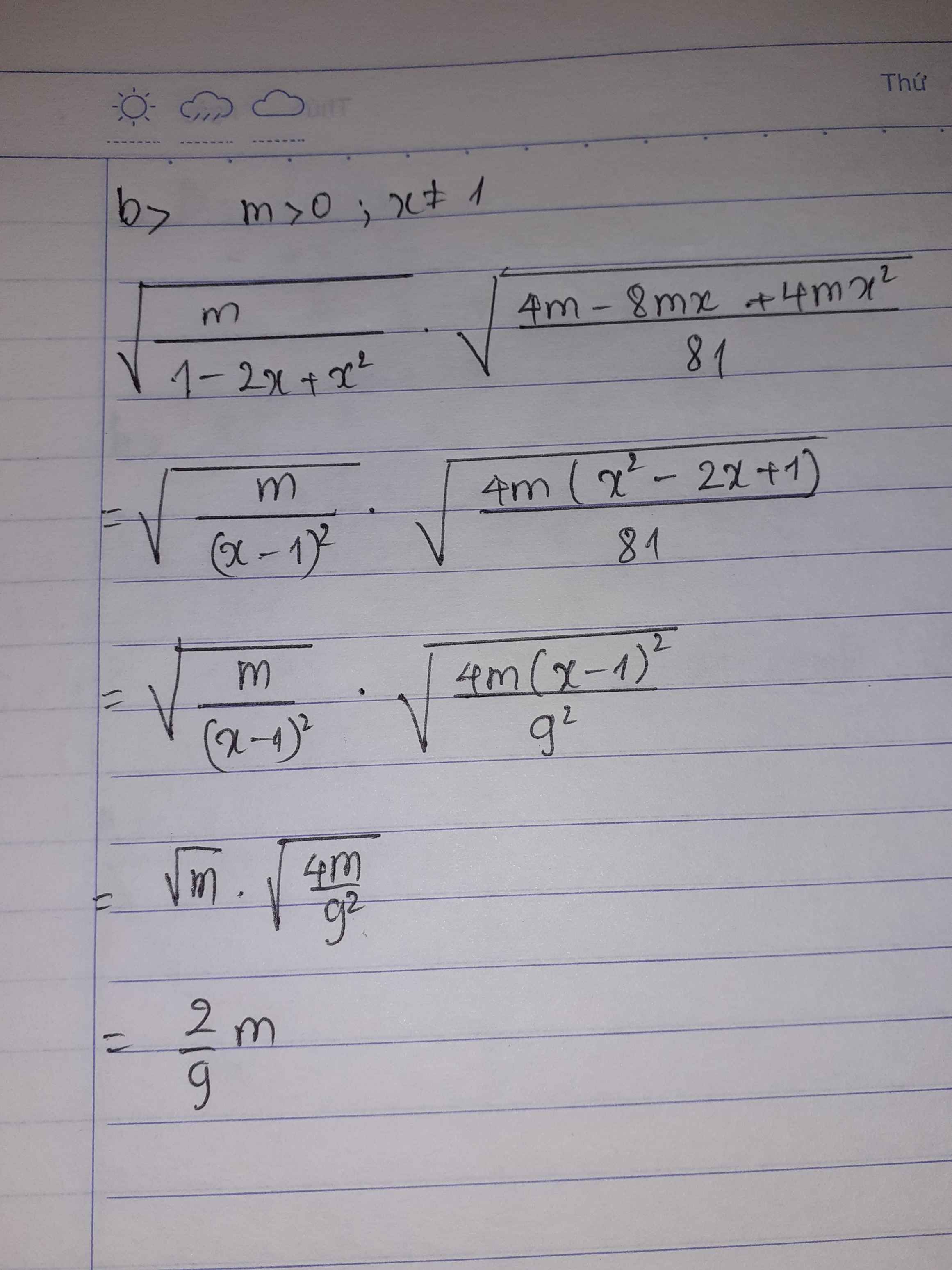
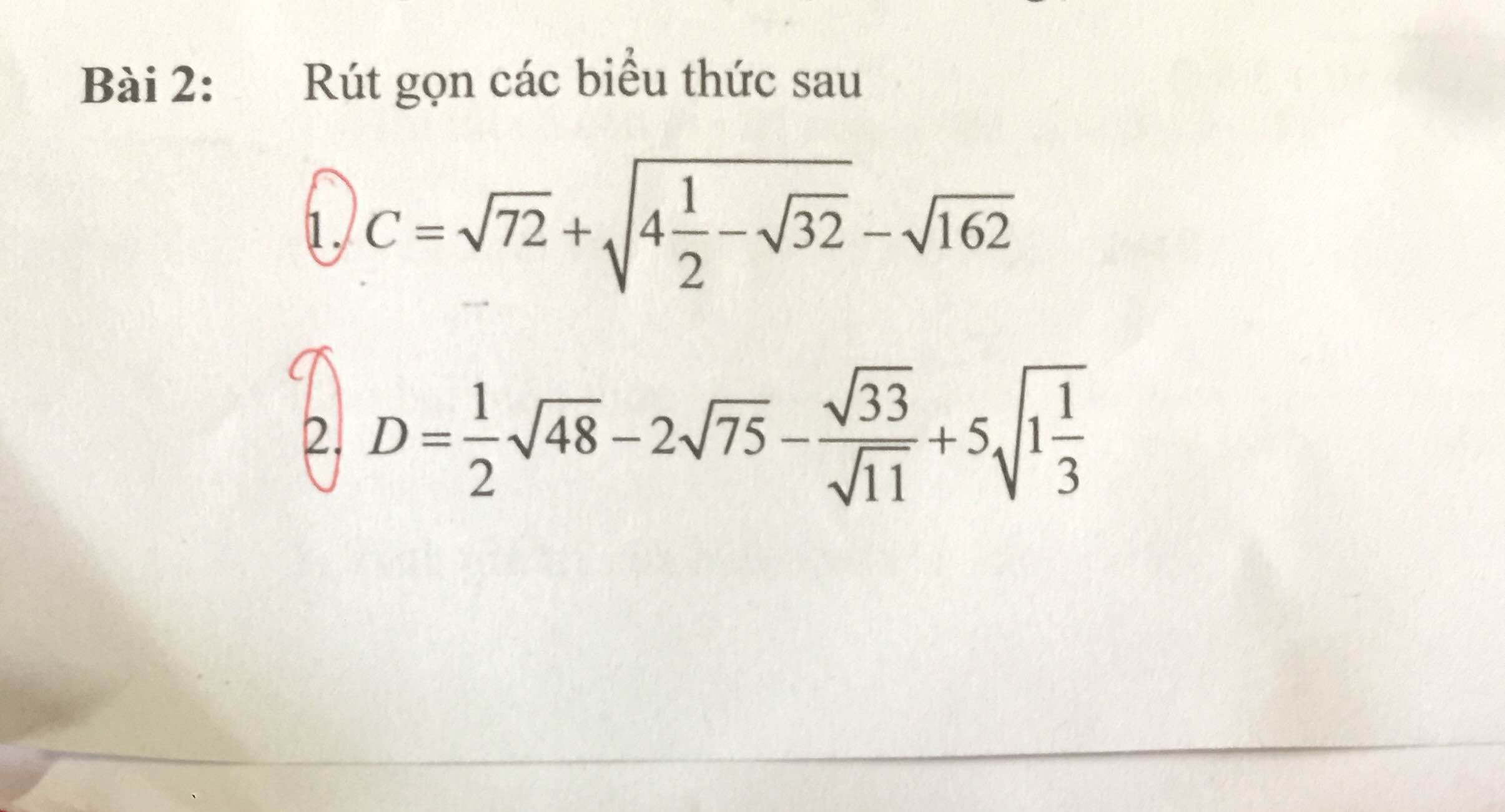
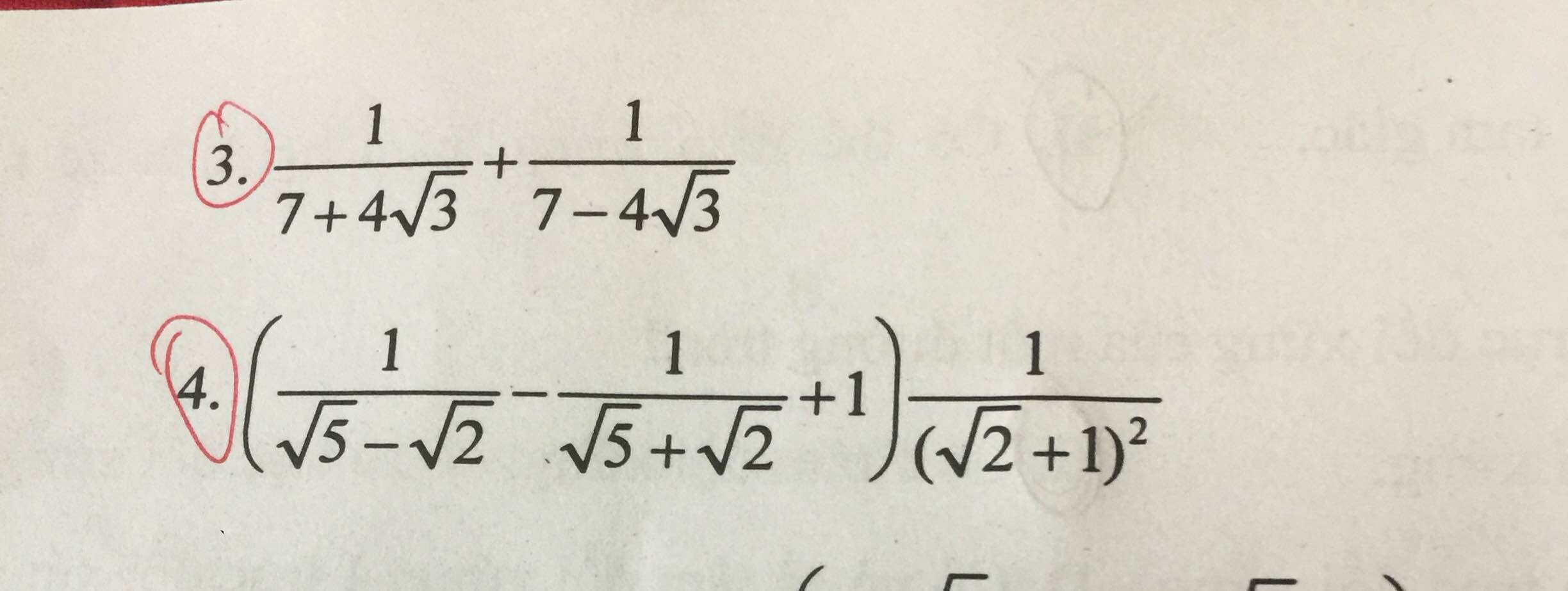

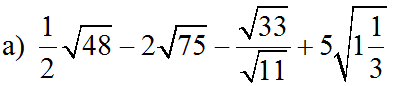

Bài 2:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5$ (cm)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{3.4}{5}=2,4$ (cm)
Áp dụng định lý Pitago:
$BH=\sqrt{AB^2-AH^2}=\sqrt{3^2-2,4^2}=1,8$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{4^2-2,4^2}=3,2$ (cm)
b.
Áp dụng hệ thức lượng trong tam giác vuông:
$AH^2=BH.CH=9.16$
$\Rightarrow AH=12$ (cm)
Áp dụng định lý Pitago:
$AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+9^2}=15$ (cm)
$AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20$ (cm)
$BC=BH+CH=9+16=25$ (cm)
Bài 3:
Vì $AB:AC=3:4$ nên đặt $AB=3a; AC=4a$ (cm)
Áp dụng định lý Pitago:
$15=BC=\sqrt{AB^2+AC^2}=\sqrt{(3a)^2+(4a)^2}=5a$
$\Rightarrow a=3$ (cm)
$AH=\frac{AB.AC}{BC}=\frac{3a.4a}{5a}=2,4a$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{(3a)^2-(2,4a)^2}=1,8a=1,8.3=5,4$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{(4a)^2-(2,4a)^2}=3,2a=3,2.3=9,6$ (cm)