Tìm a,b biết a.b =150 ; UCLN(a,b)=5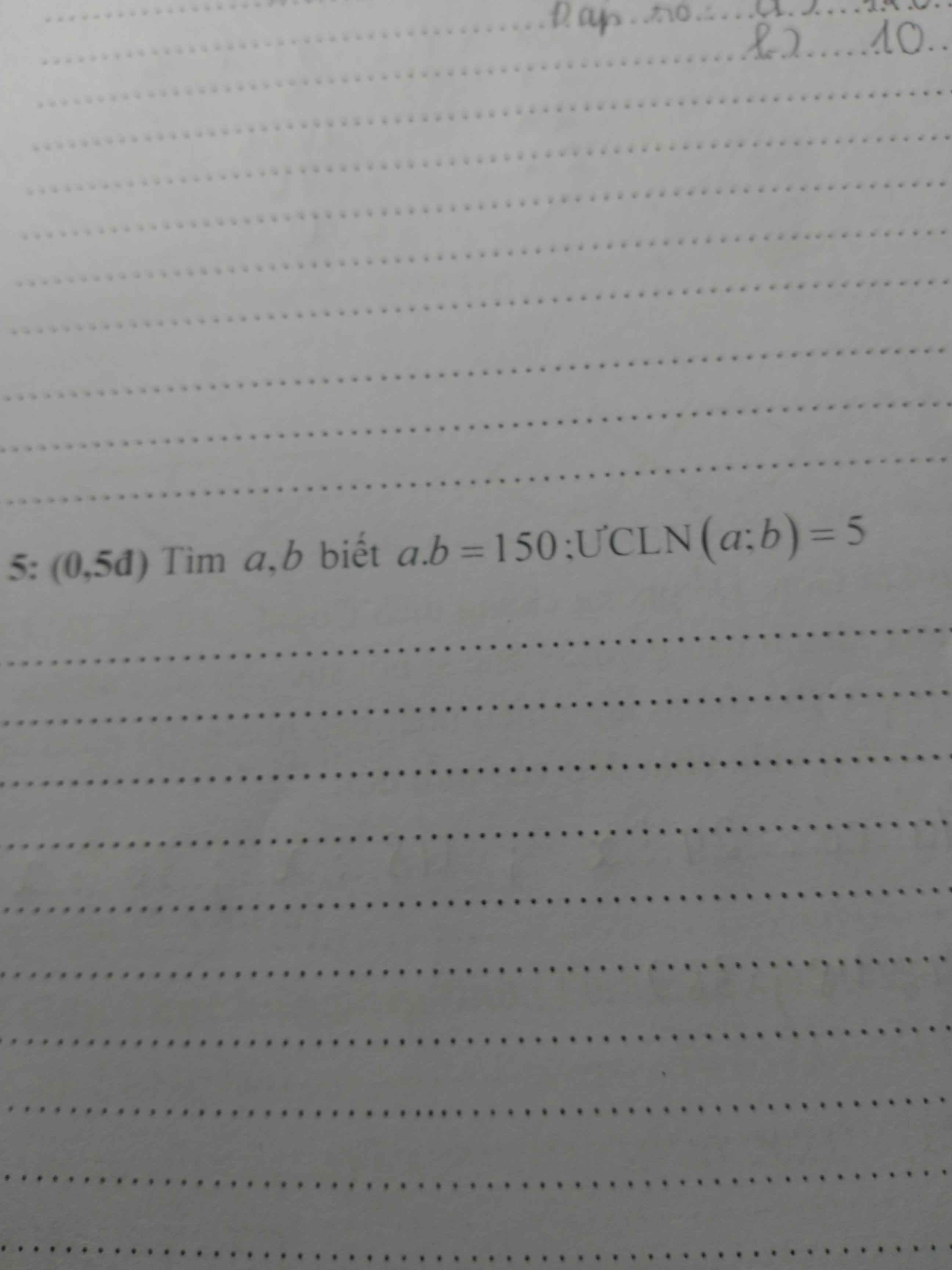
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GH
25 tháng 6 2023
Có công thức: \(ab=ƯCLN\left(a;b\right).BCNN\left(a;b\right)\)
\(\RightarrowƯCLN\left(a;b\right)=\dfrac{ab}{BCNN\left(a;b\right)}=\dfrac{180}{150}=1,2\)
\(\Rightarrow a=1,2m;b=1,2n\) (giả sử m > n)
Thay 2 giá trị a, b trên vào a.b = 180 ta được:
\(1,2m.1,2n=180\Rightarrow m.n=180:1,2^2=125\)
Có: \(125=25.5\)
Theo giả sử thì m > n => m = 25 và n = 5
\(\Rightarrow\left\{{}\begin{matrix}a=1,2m=1,2.25=30\\b=1,2n=1,2.5=6\end{matrix}\right.\)
Hoặc nếu giả sử ngược lại n > m => a = 6 và b = 30
Vậy \(\left(a;b\right)=\left(30;6\right);\left(a;b\right)=\left(6;30\right)\)
MK
2
16 tháng 11 2015
ƯCLN(a;b)=3750:150=25
Ta có: a=25.m và b=25.n với ƯCLN(m;n)=1
mặt khác: a.b=3750 \(\Rightarrow\)25.m.25.n= 3750 hay m.n=6
Nếu m=1 và n=6 thì a=25 và b=150
Nếu m=6 và n=1 thì a=150 và b=25
AH
Akai Haruma
Giáo viên
14 tháng 9
Bài 1:
\(S=\frac{abc}{abc+ab+a}+\frac{b}{bc+b+1}+\frac{a}{ab+a+abc}\\ =\frac{bc}{bc+b+1}+\frac{b}{bc+b+1}+\frac{1}{b+1+bc}=\frac{bc+b+1}{bc+b+1}=1\)
AH
Akai Haruma
Giáo viên
14 tháng 9
Bài 2:
\(\frac{a}{5}+1=\frac{1}{b-1}\\ \Rightarrow \frac{a+5}{5}=\frac{1}{b-1}\\ \Rightarrow (a+5)(b-1)=5\)
Vì $a,b$ là số tự nhiên nên $a+5, b-1$ là số nguyên. Mà tích của chúng bằng 5 nên $a+5$ là ước của $5$ (1)
Vì $a$ là số tự nhiên nên $a+5$ là số tự nhiên và $a+5\geq 5$ (2)
Từ $(1); (2)\Rightarrow a+5=5$
$\Rightarrow a=0$
$b-1=\frac{5}{5}=1\Rightarrow b=2$
PC
3
DT
1
24 tháng 10 2015
ta có:a+b=ab
=>a=ab-b
=>a=b(a-1)
=>a:b=a-1 (b khác 0)
lại có:a:b=a+b
=>a-1=a+b
=>b=-1
Do đó:a+b=ab
<=>a+(-1)=a.(-1)
<=>a-1=-a
=>2a=1=>a=1/2=0,5
tick đi bn!
HQ
0
EL
2
H
30 tháng 4 2016
Ta có \(\sqrt[3]{a}.\sqrt[3]{b}=2Haisố\sqrt[3]{a},\sqrt[3]{b}cầntìmlànghiệmcủapt\)
x2-3x+2 Ta có a +b+c =1-3+2 =0 =>x1 = 1 x2=c/a =2
Vậy \(\sqrt[3]{a}=1hoặc\sqrt[3]{a}=2;\sqrt[3]{b}=1hoặc\sqrt[3]{b}=2\)Suy ra a =1 hoặc a = 8 b=1 hoặc b=8
Vì \(ƯCLN\left(a,b\right)=5\Rightarrow\left\{{}\begin{matrix}a=5k\\b=5q\end{matrix}\right.\left(k,q\in N\text{*}\right)\)
Ta có \(ab=150\Rightarrow25kq=150\Rightarrow kq=6\)
Mà \(\left(k,q\right)=1\)
\(\Rightarrow\left(k,q\right)\in\left\{\left(1;6\right);\left(6;1\right);\left(2;3\right);\left(3;2\right)\right\}\\ \Rightarrow\left(a;b\right)\in\left\{\left(5;30\right);\left(30;5\right);\left(10;15\right);\left(15;10\right)\right\}\)