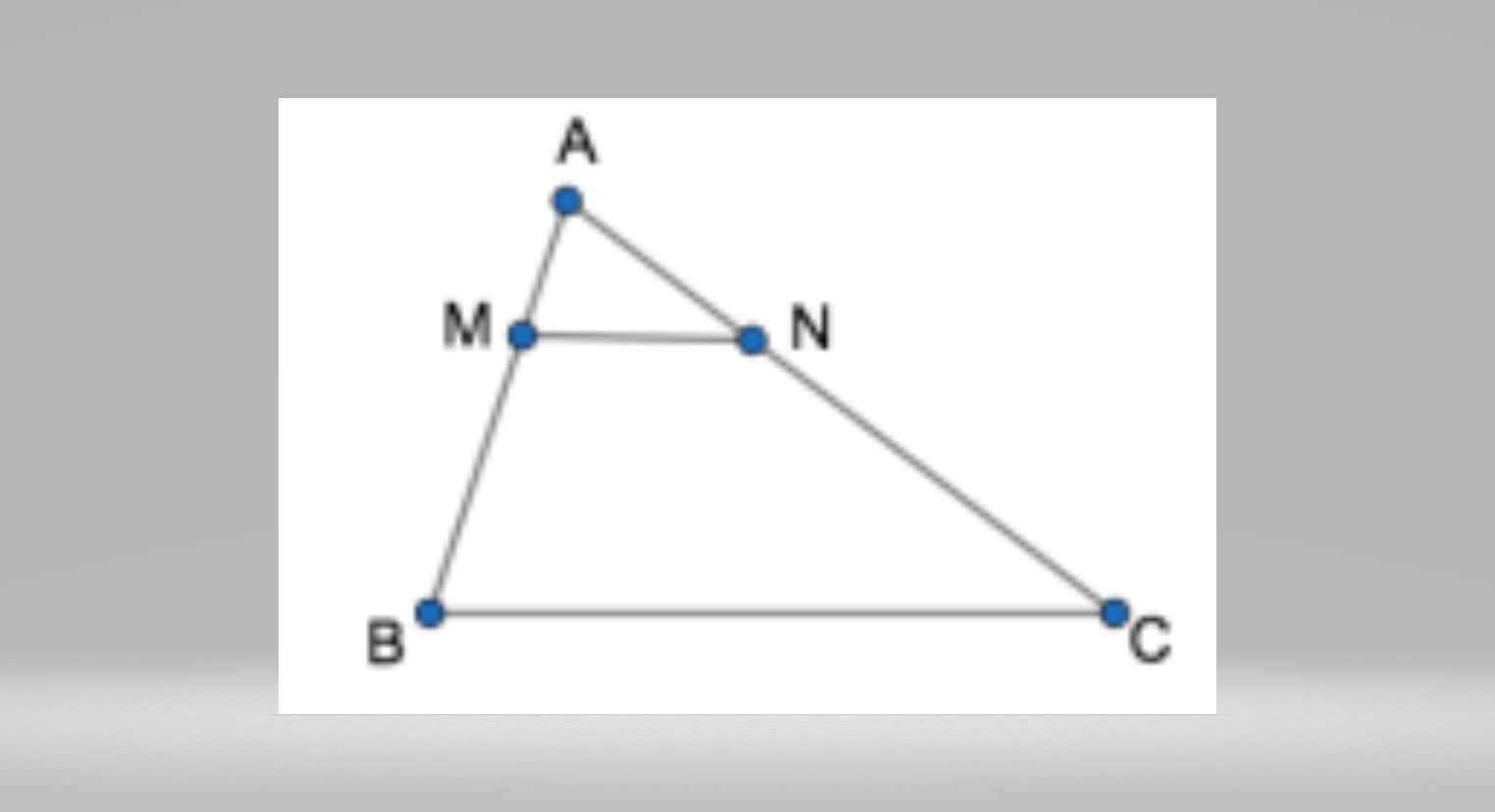
Cho tam giác ABC như hình vẽ
bên. BiếtAM=1/3 x AB; AN = 1/3 x AC và diện
tích tam giác AMN là 6cm2. Tính diện
tích tam giác ABC.
 kho qua !!!!!11 giup minh nha!!
kho qua !!!!!11 giup minh nha!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/
Hai tg BPQ và tg CQP có đường cao từ B->PQ = đường cao từ C->PQ
Cạnh đáy PQ chung
\(\Rightarrow S_{BPQ}=S_{CQP}\)
Hai tg trên có phần diện tích chung là \(S_{IPQ}\Rightarrow S_{BIP}=S_{QIC}\)
b/
Hai tg ACP và tg ABC có chung đường cao từ C->AB nên
\(\dfrac{S_{ACP}}{S_{ABC}}=\dfrac{AP}{AB}=\dfrac{1}{3}\Rightarrow S_{ACP}=\dfrac{1}{3}xS_{ABC}\)
Hai tg ACP và tg ABQ có phần diện tích chung là \(S_{APIQ}\)
Mà \(S_{BIP}=S_{QIC}\Rightarrow S_{ACP}=S_{ABQ}=\dfrac{1}{3}xS_{ABC}\)
Hai tg APQ và tg ABQ có chung đường cao từ Q->AB nên
\(\dfrac{S_{APQ}}{S_{ABQ}}=\dfrac{AP}{AB}=\dfrac{1}{3}\Rightarrow S_{APQ}=\dfrac{1}{3}xS_{ABQ}=\dfrac{1}{3}x\dfrac{1}{3}xS_{ABC}=\dfrac{1}{9}xS_{ABC}\)
\(\Rightarrow S_{BPQC}=S_{ABC}-S_{APQ}=S_{ABC}-\dfrac{1}{9}xS_{ABC}=\dfrac{8}{9}xS_{ABC}=\dfrac{8}{9}x45=40cm^2\)

bn tham khảo:
a) Diện tich tam giác ABC là :
7,2 x 7,5 : 2 = 27 ( cm2 )
b) Nối P với C
Xét hai tam giác APC và ABC
Chung chiều cao hạ từ đỉnh C xuống cạnh AB
PA = 2/3 AB
=> SAPC = SABC x 2/3 = 27 x 2/3 = 18 ( cm2 )
Xét 2 tam giác APQ và APC
Chung chiều cao hạ từ đỉnh P xuống cạnh AC
AQ = 1/4 AC
=> SAPQ = SAPC X 1/4 = 18 x 1/4 = 4,5 ( cm2 )
Đáp số : 4,5 cm2

\(AM=\dfrac{1}{2}AB\)
=>\(S_{AMC}=\dfrac{1}{2}\cdot S_{ABC}=\dfrac{1}{2}\cdot27=13,5\left(cm^2\right)\)
Vì \(AN=\dfrac{1}{3}AC\)
nên \(S_{AMN}=\dfrac{1}{3}\cdot S_{AMC}=\dfrac{1}{3}\cdot13,5=4,5\left(cm^2\right)\)

a) Ta có: \(\frac{{A'B'}}{{AB}} = \frac{2}{6} = \frac{1}{3},\frac{{A'C'}}{{AC}} = \frac{3}{9} = \frac{1}{3},\frac{{B'C'}}{{BC}} = \frac{4}{{12}} = \frac{1}{3}\). Do đó, các tỉ số trên bằng nhau.
b) Ta có: \(\frac{{AM}}{{AB}} = \frac{2}{6} = \frac{1}{3};\frac{{AN}}{{AC}} = \frac{3}{9} = \frac{1}{3}\)
Vì \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} \Rightarrow MN//BC\) (định lí Thales đảo)
Vì \(MN//BC \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\) (Hệ quả của định lí Thales)
Do đó, \(\frac{{MN}}{{BC}} = \frac{1}{3} \Leftrightarrow \frac{{MN}}{{12}} = \frac{1}{3} \Rightarrow MN = \frac{{12.1}}{3} = 4\).
Vậy \(MN = 4cm\).
c) Vì \(MN//BC \Rightarrow \Delta ABC\backsim\Delta AMN\) (định lí)(1)
Xét tam giác \(AMN\) và tam giác \(A'B'C'\) ta có:
\(AM = A'B' = 2cm;AN = A'C' = 2cm;MN = B'C' = 4cm\)
Do đó, \(\Delta AMN = \Delta A'B'C'\) (c.c.c)
Vì \(\Delta AMN = \Delta A'B'C'\) nên \(\Delta AMN\backsim\Delta A'B'C'\) (2)
Từ (1) và (2) suy ra, \(\Delta ABC\backsim\Delta A'B'C'\).

ABD và BDE có Ab=BE , và có chung cạnh BD
=> ABD =BED =9cm2
DC=1/3 BC => DC=1/2 BD
ABD và ACD có DC=1/2 BD và chung đường cao hạ từ đỉnh C
=> ADC = 1/2 ABD = 1/2x9=4,5cm2
=> S. ABC = 9+4,5=13,5cm2
hong bé ơi, iem có follow anh gòi nhưng mà anh hok bíc làm nha bé:)))
ngay mai tui giet baaaaaaaaaa!!!!!