Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho hình thang ABCD đáy nhỏ AB đáy lớn CD. Hai đường chéo AC và BD cắt nhau tại G. Biết diện tích tam giác AGD bằng và diện tích tam giác CGD bằng Tính diện tích hình thang ABCD.
Trả lời: Diện tích hình thang ABCD là
(Nhập kết quả dưới dạng số thập phân gọn nhất)Cho hình thang ABCD đáy nhỏ AB đáy lớn CD. Hai đường chéo AC và BD cắt nhau tại G. Biết diện tích tam giác AGD bằng và diện tích tam giác CGD bằng Tính diện tích hình thang ABCD.
Trả lời: Diện tích hình thang ABCD là 73,96 cm2
Cho hình thang ABCD đáy nhỏ AB đáy lớn CD. Hai đường chéo AC và BD cắt nhau tại G. Biết diện tích tam giác AGD bằng và diện tích tam giác CGD bằng Tính diện tích hình thang ABCD.
Trả lời: Diện tích hình thang ABCD là
(Nhập kết quả dưới dạng số thập phân gọn nhất)Cho hình thang ABCD đáy nhỏ AB đáy lớn CD. Hai đường chéo AC và BD cắt nhau tại G. Biết diện tích tam giác AGD bằng và diện tích tam giác CGD bằng Tính diện tích hình thang ABCD.
Trả lời: Diện tích hình thang ABCD là
(Nhập kết quả dưới dạng số thập phân gọn nhất)

ta biết số tự nhiên lớn nhất có 2 chữ số là 99 nhưng 99 không chia hết cho 2
=>2a=98
=>a=98:2
=.a=49
vậy ông ấy đã viết 49 cuốn sách
- Số tự nhiên lớn nhất có 2 chữ số là: 99.
Vậy ông đã viết đc 992 cuốn sách.
Chọn mk nha ^_^

anh mình thấy mình cứ online nên nhờ mình vào đây hỏi không ai giúp thì để mình xóa
gọi d = (a2; a+ b)
=> a2 chia hết cho d và a+ b chia hết cho d
a2 chia hết cho d => a chia hết cho d
=> b = (a+b) - a chia hết cho d
=> d \(\in\) ƯC(a; b) => d \(\le\) (a;b) = 1 => d = 1
Vậy .......
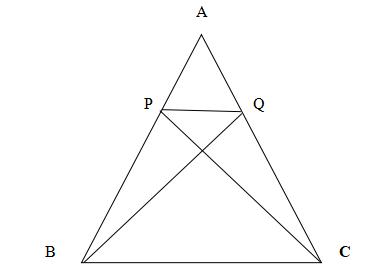
a/
Hai tg BPQ và tg CQP có đường cao từ B->PQ = đường cao từ C->PQ
Cạnh đáy PQ chung
\(\Rightarrow S_{BPQ}=S_{CQP}\)
Hai tg trên có phần diện tích chung là \(S_{IPQ}\Rightarrow S_{BIP}=S_{QIC}\)
b/
Hai tg ACP và tg ABC có chung đường cao từ C->AB nên
\(\dfrac{S_{ACP}}{S_{ABC}}=\dfrac{AP}{AB}=\dfrac{1}{3}\Rightarrow S_{ACP}=\dfrac{1}{3}xS_{ABC}\)
Hai tg ACP và tg ABQ có phần diện tích chung là \(S_{APIQ}\)
Mà \(S_{BIP}=S_{QIC}\Rightarrow S_{ACP}=S_{ABQ}=\dfrac{1}{3}xS_{ABC}\)
Hai tg APQ và tg ABQ có chung đường cao từ Q->AB nên
\(\dfrac{S_{APQ}}{S_{ABQ}}=\dfrac{AP}{AB}=\dfrac{1}{3}\Rightarrow S_{APQ}=\dfrac{1}{3}xS_{ABQ}=\dfrac{1}{3}x\dfrac{1}{3}xS_{ABC}=\dfrac{1}{9}xS_{ABC}\)
\(\Rightarrow S_{BPQC}=S_{ABC}-S_{APQ}=S_{ABC}-\dfrac{1}{9}xS_{ABC}=\dfrac{8}{9}xS_{ABC}=\dfrac{8}{9}x45=40cm^2\)