Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

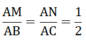
⇒ MN // BC (định lí Ta lét đảo)
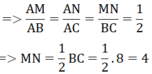
Suy ra: Δ AMN = ∆ A’B’C’(c.c.c) nên hai tam giác này cũng đồng dạng với nhau (1).
Xét tam giác ABC có MN// BC nên Δ AMN đồng dạng với tam giác ABC (2)
Từ (1) và (2) suy ra: Δ A’B’C’ đồng dạng với tam giác ABC (tính chất).

Bổ sung đề: AB=6cm; AC=9cm
a: Xét ΔABC có AM/AB=AN/AC
nên MN//BC
b: Ba tam giác này đồng dạng với nhau

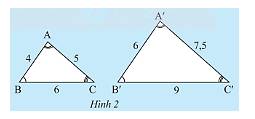
a) Từ kí hiệu của hình vẽ ta thấy các cặp góc bằng nhau là:
\(\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\)
b) Ta có:
\(\frac{{A'B'}}{{AB}} = \frac{6}{4} = \frac{3}{2};\frac{{A'C'}}{{AC}} = \frac{{7,5}}{5} = \frac{3}{2};\frac{{B'C'}}{{BC}} = \frac{9}{6} = \frac{3}{2}\).
Ta thấy, \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{3}{2}\)
a: góc A=góc A'; góc B=góc B'; góc C=góc C'
b: A'B'/AB=A'C'/AC=B'C'/BC

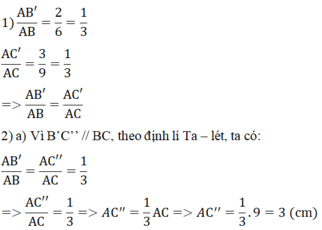
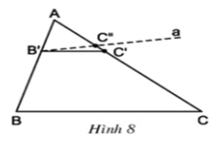
b) Trên đoạn thẳng AC ta có: AC’= AC’’= 3 cm nên
Khi đó, hai đường thẳng BC và B’C’ song song với nhau.

a) Xét ∆ABC và ∆A'B'C' ta có :
AB = A'B'
B'A'C' = BAC
AC = A'C'
=> ∆ABC = ∆A'B'C' (c.g.c)
b) Xét ∆AMC và ∆A'M'C' ta có :
AM = A'M'
BAC = B'A'C'
AC = A'C'
=> ∆AMC = ∆A'M'C' (c.g.c)
c) Ta có :
A'M' + M'B' = A'B'
AM + MB = AB
Mà AM = A'M' , A'B' = AB
=> BM = B'M
d) Vì ∆ABC = ∆A'B'C' (cmt)
=> ABC = A'B'C'
Xét ∆MBE và ∆M'B'E' ta có :
MB = M'B'
ABC = A'B'C'
BE = B'E'
=> ∆MBE = ∆M'B'E' (c.g.c)

a)
i) Vì \(OA' = 3OA \Rightarrow \frac{{OA}}{{OA'}} = \frac{1}{3}\);\(OB' = 3OB \Rightarrow \frac{{OB}}{{OB'}} = \frac{1}{3}\).
Xét tam giác \(OA'B'\) có:
\(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{1}{3}\)
Do đó, \(A'B'//AB\) (định lí Thales đảo)
ii) Vì \(A'B'//AB \Rightarrow \frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{AB}}{{A'B'}} = \frac{1}{3}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{A'B'}}{{AB}} = \frac{3}{1} = 3\).
b)
i)
- Vì \(OA' = 3OA \Rightarrow \frac{{OA}}{{OA'}} = \frac{1}{3}\);\(OB' = 3OB \Rightarrow \frac{{OB}}{{OB'}} = \frac{1}{3}\).
Xét tam giác \(OA'B'\) có:
\(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{1}{3}\)
Do đó, \(A'B'//AB\) (định lí Thales đảo)
Vì \(A'B'//AB \Rightarrow \frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{AB}}{{A'B'}} = \frac{1}{3}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{A'B'}}{{AB}} = \frac{3}{1} = 3\).
- Vì \(OA' = 3OA \Rightarrow \frac{{OA}}{{OA'}} = \frac{1}{3}\);\(OC' = 3OC \Rightarrow \frac{{OC}}{{OC'}} = \frac{1}{3}\).
Xét tam giác \(OA'C'\) có:
\(\frac{{OA}}{{OA'}} = \frac{{OC}}{{OC'}} = \frac{1}{3}\)
Do đó, \(A'C'//AC\) (định lí Thales đảo)
Vì \(A'C'//AC \Rightarrow \frac{{OA}}{{OA'}} = \frac{{OC}}{{OC'}} = \frac{{AC}}{{A'C'}} = \frac{1}{3}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{A'C'}}{{AC}} = \frac{3}{1} = 3\).
- Vì \(OB' = 3OB \Rightarrow \frac{{OB}}{{OB'}} = \frac{1}{3}\);\(OC' = 3OC \Rightarrow \frac{{OC}}{{OC'}} = \frac{1}{3}\).
Xét tam giác \(OB'C'\) có:
\(\frac{{OB}}{{OB'}} = \frac{{OC}}{{OC'}} = \frac{1}{3}\)
Do đó, \(B'C'//BC\) (định lí Thales đảo)
Vì \(B'C'//BC \Rightarrow \frac{{OB}}{{OB'}} = \frac{{OC}}{{OC'}} = \frac{{BC}}{{B'C'}} = \frac{1}{3}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{B'C'}}{{BC}} = \frac{3}{1} = 3\).
Do đó, \(\frac{{B'C'}}{{BC}} = \frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\)
ii) Xét tam giác \(A'B'C'\) và tam giác \(ABC\) ta có:
\(\frac{{B'C'}}{{BC}} = \frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) (chứng minh trên)
Do đó, tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\).
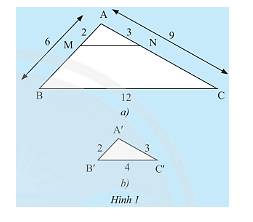
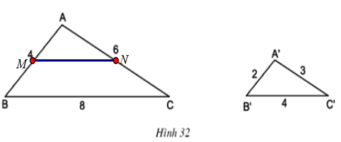
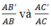


a) Ta có: \(\frac{{A'B'}}{{AB}} = \frac{2}{6} = \frac{1}{3},\frac{{A'C'}}{{AC}} = \frac{3}{9} = \frac{1}{3},\frac{{B'C'}}{{BC}} = \frac{4}{{12}} = \frac{1}{3}\). Do đó, các tỉ số trên bằng nhau.
b) Ta có: \(\frac{{AM}}{{AB}} = \frac{2}{6} = \frac{1}{3};\frac{{AN}}{{AC}} = \frac{3}{9} = \frac{1}{3}\)
Vì \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} \Rightarrow MN//BC\) (định lí Thales đảo)
Vì \(MN//BC \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\) (Hệ quả của định lí Thales)
Do đó, \(\frac{{MN}}{{BC}} = \frac{1}{3} \Leftrightarrow \frac{{MN}}{{12}} = \frac{1}{3} \Rightarrow MN = \frac{{12.1}}{3} = 4\).
Vậy \(MN = 4cm\).
c) Vì \(MN//BC \Rightarrow \Delta ABC\backsim\Delta AMN\) (định lí)(1)
Xét tam giác \(AMN\) và tam giác \(A'B'C'\) ta có:
\(AM = A'B' = 2cm;AN = A'C' = 2cm;MN = B'C' = 4cm\)
Do đó, \(\Delta AMN = \Delta A'B'C'\) (c.c.c)
Vì \(\Delta AMN = \Delta A'B'C'\) nên \(\Delta AMN\backsim\Delta A'B'C'\) (2)
Từ (1) và (2) suy ra, \(\Delta ABC\backsim\Delta A'B'C'\).