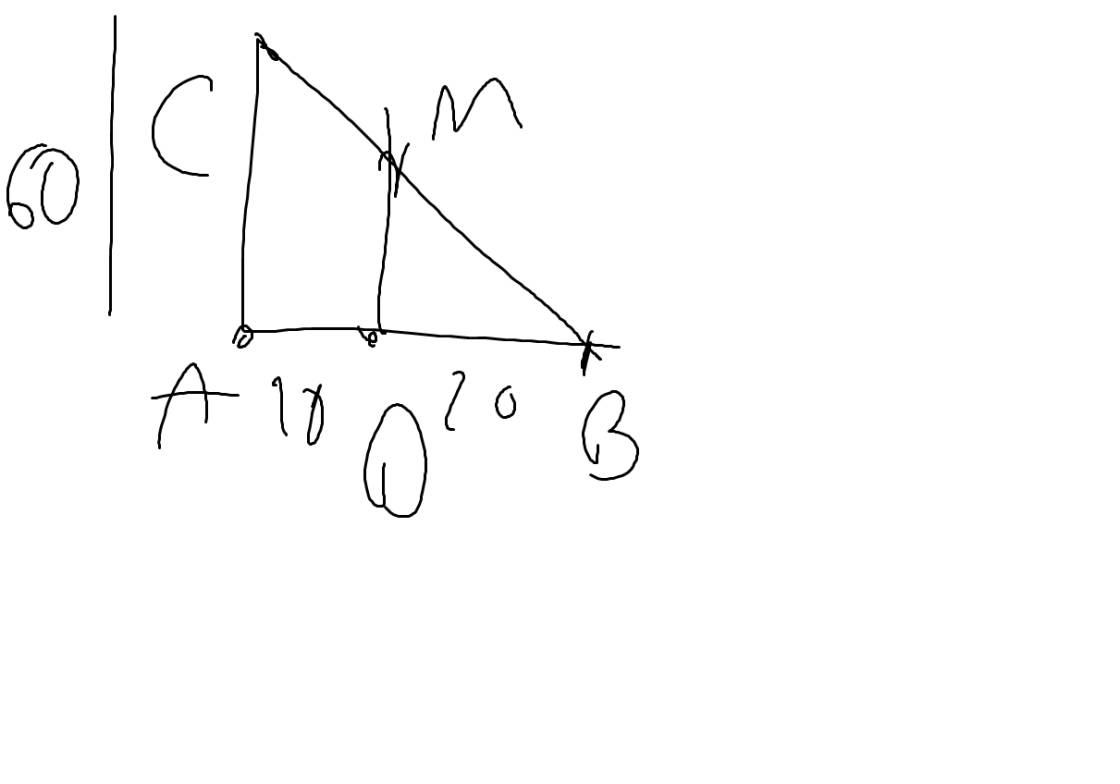Cho tam giác vuông ABC (góc a = 900) có AB=30cm; AC=40cm. AE là đường cao và BD là phân giác của tam giác. Gọi F là giao điểm của AE và BD
a) Chứng minh tam giác ABC đồng dạng tam giác EBA
b) Chứng minh BD.EF=BF.AD
c) Tính AD
d) Chứng minh FA/EF=DC/DA