Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
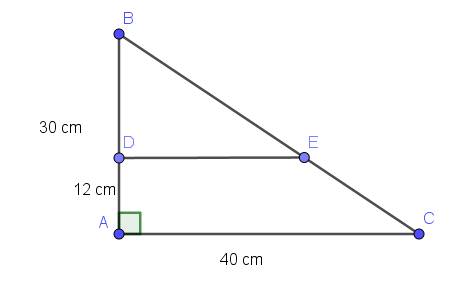
$BD=AB-DA=30-12=18$ (cm)
Diện tích tam giác ABC:
$AB.AC:2=30.40:2=600$ (cm2)
Diện tích tam giác ABC cũng bằng;
$S_{BDE}+S_{ADEC}=BD.DE:2+(DE+AC).AD:2$
$=18.DE:2+(DE+40).12:2$
$=9DE+6(DE+40)$ (cm2)
Vậy: $600=9DE+6(DE+40)=15DE+240$
$\Rightarrow DE=(600-240):15=24$ (cm)
Diện tích hình thang DECA:
$(DE+AC).DA:2=(24+40).12:2=384$ (cm2)


Hình bạn tự vẽ nha
a)Ta có : BM=BA-AM=30-20=10(cm)
Diện tích tam giác BCM là
S=\(\frac{BM.AC}{2}\)=\(\frac{10.36}{2}\)=180\(cm^2\)
b) Mình làm theo Dịnh lí Ta- lét trong tam giác ABC có MN//BC có:
\(\frac{AM}{AB}=\frac{AN}{AC}\)
<=>\(\frac{20}{30}=\frac{AN}{36}\)
<=>AN=24(cm)
Tứ đó ta có Sbcnm=Sbac-Samn=\(\frac{30.36}{2}\)-\(\frac{24.20}{2}\)=540-240=300(\(cm^2\))

Diện tích tam giác ABC = 60 x 30 : 2 = 900 (cm2)
Diện tích tam giác BKA = 2323 diện tích tam giác BAC
(vì cùng đường cao hạ từ B xuống AC và đáy KA = 2323AC)
Diện tích tam giác BKA là: 900×23= 600900×23= 600 (cm2)
Nối EK ta có:
Diện tích tam giác AEG = Diện tích tam giác EGK
(cùng đường cao hạ Từ E xuống AK. Đáy GA = GK)
Và diện tích tam giác KED = diện tích tam giác KDB
(Vì cùng đường cao hạ từ K xuống EB và đáy DE = DB)
Do đó:
Diện tích tam giác EGK + diện tích tam giác KED = diện tích tam giác EAG + diện tích tam giác KDB = 1212 diện tích tam giác BAK
Vậy diện tích tam giác EGK + diện tích tam giác KED = 600 : 2 = 300 (cm2)
Hay diện tích hình DEKG = 300 cm2

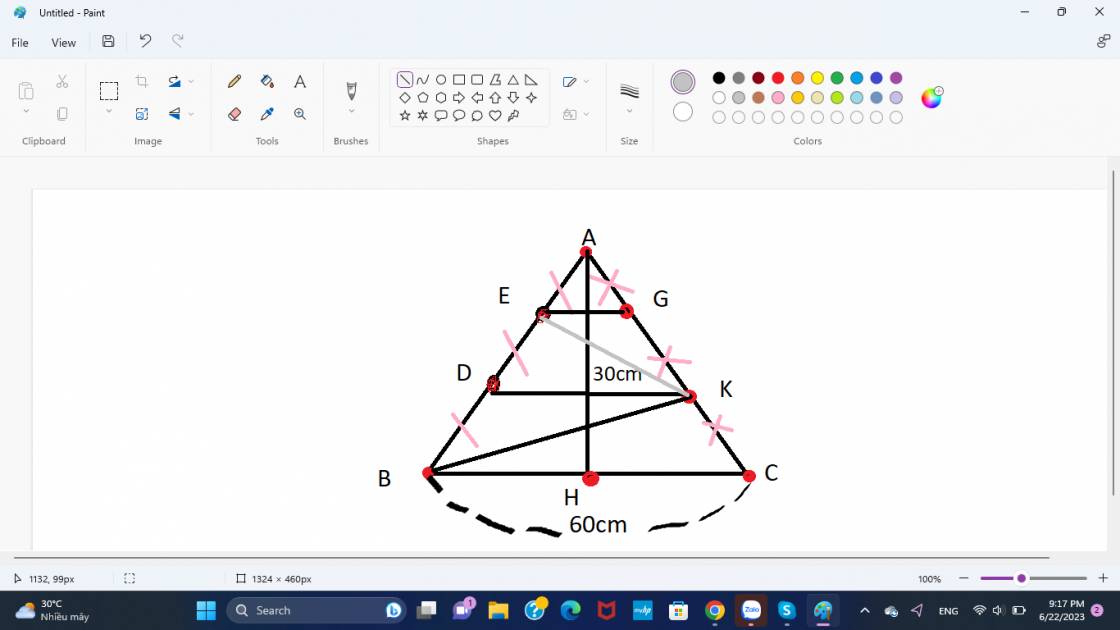
a) SABC : 60.30 :2 = 900(cm2)
b) Nối điểm E với điểm K
Ta có:
SEDK = SBDK ( vì chiều cao của 2 hình đều = \(\dfrac{1}{3}AH\) và đều hạ xuống đáy DK)
SEAG = SKDB ( vì chiều cao của 2 hình đều = \(\dfrac{1}{3}AH\) và đều hạ xuống đáy EG)
=> SEGK + SKED = SEAG + SKDB = \(\dfrac{1}{2}S_{BAK}\)
=> SDEGK = \(\dfrac{1}{2}S_{BAK}\)
\(\dfrac{S_{DEGK}}{S_{BAK}}=\dfrac{1}{2}\)
a) SABC : 60.30 :2 = 900(cm2)
b) Nối điểm E với điểm K
Ta có:
SEDK = SBDK ( vì chiều cao của 2 hình đều = 13��31AH và đều hạ xuống đáy DK)
SEAG = SKDB ( vì chiều cao của 2 hình đều = 13��31AH và đều hạ xuống đáy EG)
=> SEGK + SKED = SEAG + SKDB = 12����21SBAK
=> SDEGK = 12����21SBAK
���������=12SBAKSDEGK=21
MDAC là hình thang có chiều cao 10cm
=>MD//AC và AD=10cm
DB+AD=AB
=>DB+10=30
=>DB=20(cm)
Xét ΔBAC có MD//AC
nên \(\dfrac{MD}{AC}=\dfrac{BD}{BA}\)
=>\(\dfrac{MD}{60}=\dfrac{20}{30}=\dfrac{2}{3}\)
=>\(MD=60\cdot\dfrac{2}{3}=40\left(cm\right)\)
Diện tích hình thang ADMC là:
\(S_{ADMC}=\dfrac{1}{2}\cdot AD\cdot\left(MD+AC\right)\)
\(=\dfrac{1}{2}\cdot10\cdot\left(60+40\right)=5\cdot100=500\left(cm^2\right)\)
Diện tích tam giác ABC là:
\(S_{ACB}=\dfrac{1}{2}\cdot AB\cdot AC=900\left(cm^2\right)\)
\(S_{ABC}=S_{BMD}+S_{CMDA}\)
=>\(S_{BMD}+500=900\)
=>\(S_{DMB}=400\left(cm^2\right)\)