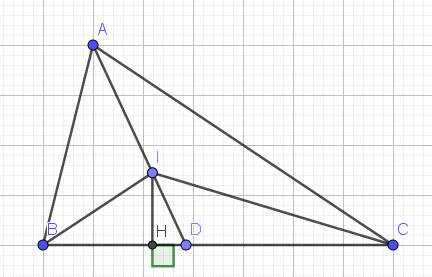
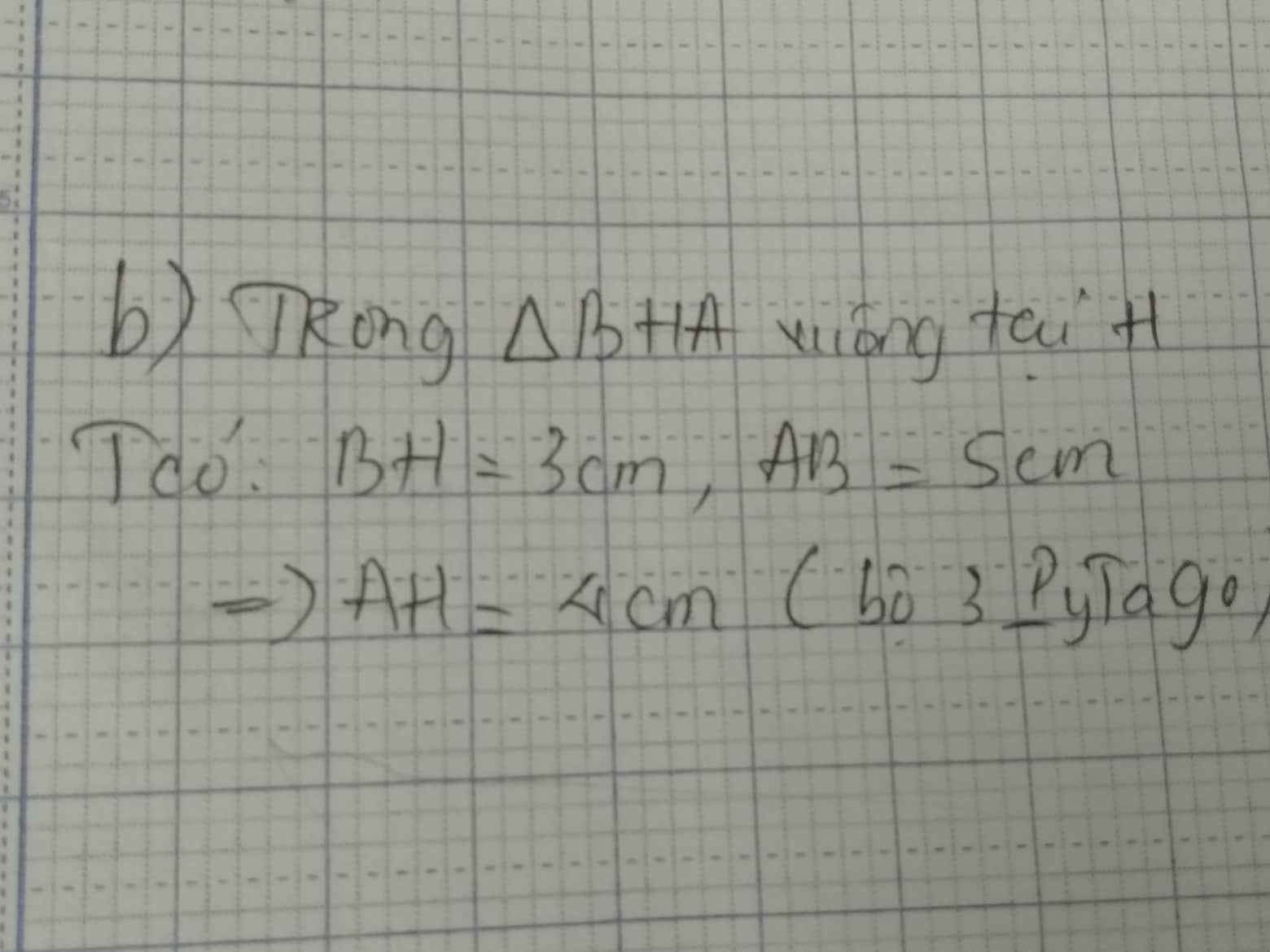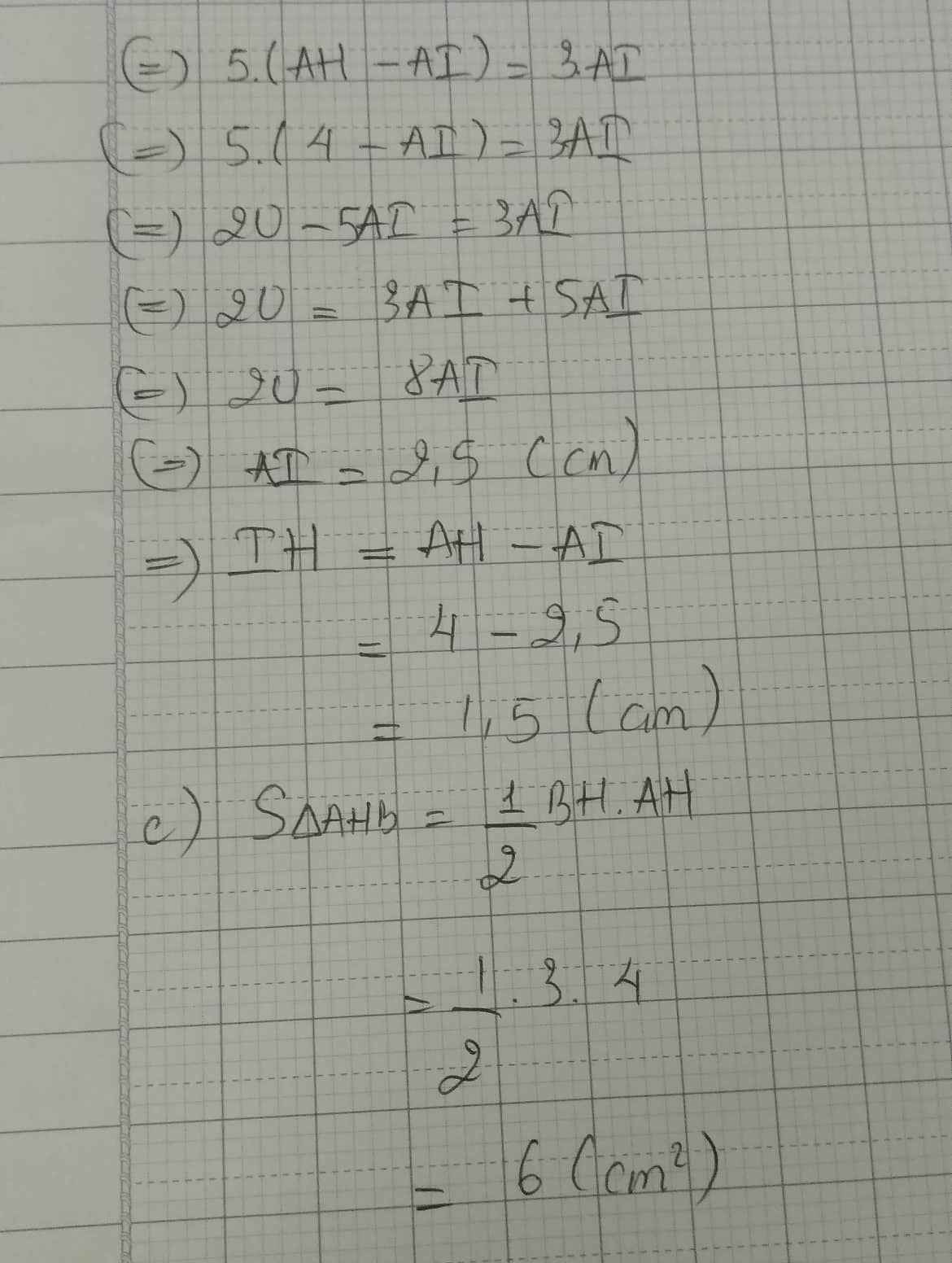tam giác ABC, I;O lần lượt là tâm dường tròn nội tiếp,ngoại tiếp tam giác; G là trọng trong tâm. CMR: Nếu goc AIO=90 độ thì IG // BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


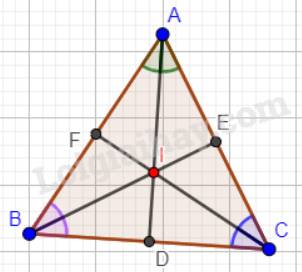
Ta có: I là giao điểm của ba đường phân giác của tam giác ABC. Đồng thời là giao điểm của ba đường trung trực tam giác ABC nên: \(ID \bot BC;IE \bot AC;IF \bot AB\).
Xét tam giác ADB và tam giác ADC có:
\(\widehat {BAD} = \widehat {CAD}\)(AD là phân giác của góc A);
AD chung;
\(\widehat {ADB} = \widehat {ADC}(=90^0)\)(vì \(ID \bot BC\)).
Vậy \(\Delta ADB = \Delta ADC\)(g.c.g). Suy ra: AB = AC ( 2 cạnh tương ứng). (1)
Tương tự ta có: \(\Delta BEA = \Delta BEC\)(g.c.g). Suy ra: BA = BC ( 2 cạnh tương ứng). (2)
Từ (1) và (2) suy ra: AB = BC = AC.
Vậy tam giác ABC đều.

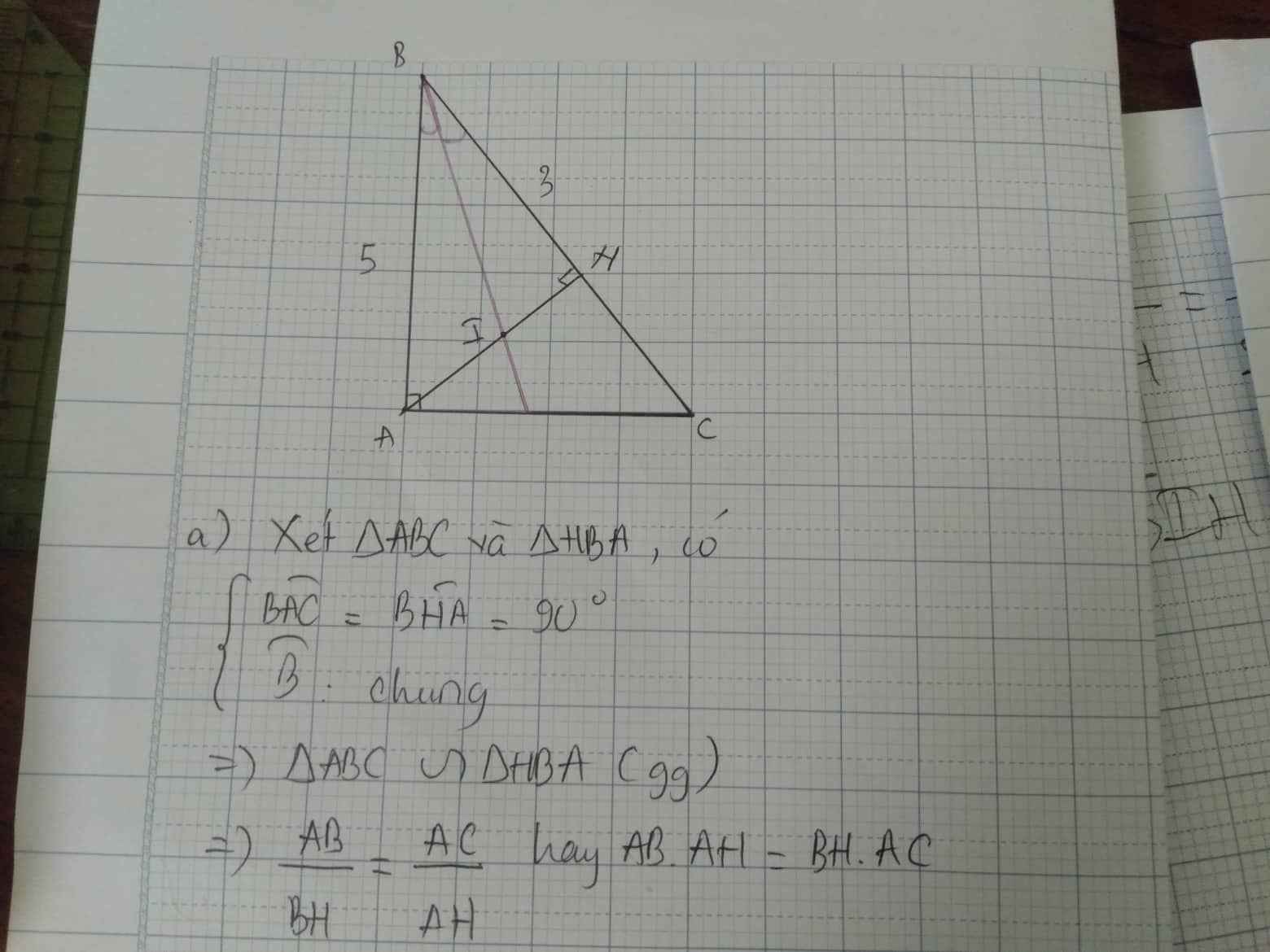
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>AB/HB=AC/HA
=>AB*HA=HB*AC
b: BC=căn 9^2+12^2=15cm
BI là phân giác
=>AI/AB=CI/BC
=>AI/3=CI/5=12/8=1,5
=>AI=4,5cm
c: S HAB/S HCA=(AB/CA)^2

Lời giải:
Ta thấy:
$\widehat{BID}=180^0-\widehat{BIA}=\widehat{ABI}+\widehat{BAI}$
$=\frac{\widehat{B}}{2}+\frac{\widehat{A}}{2}=\frac{\widehat{A}+\widehat{B}}{2}$
$=\frac{180^0-\widehat{C}}{2}=90^0-\widehat{C}.\frac{1}{2}$
$=90^0-\widehat{ICH}=\widehat{CIH}$
Vậy:
$\widehat{BID}=\widehat{CIH}$
$\Rightarrow \widehat{BIH}+\widehat{HID}=\widehat{HID}+\widehat{CID}$
$\Rightarrow \widehat{BIH}=\widehat{CID}$ (đpcm)