Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Gọi D, E, F lần lượt là chân các đường phân giác của tam giác ABC lần lượt hạ từ A, B, C.
Gọi T là trung điểm của BC. Do AD là đường phân giác của tam giác ABC nên \(\frac{BD}{AB}=\frac{CD}{AC}\Rightarrow\frac{BD}{5}=\frac{CD}{7}=\frac{BD+CD}{5+7}=\frac{6}{12}=\frac{1}{2}\)\(\Rightarrow\hept{\begin{cases}BD=2,5\\CD=3,5\end{cases}}\)
\(\Delta ABD\) có BI là đường phân giác nên \(\frac{AI}{ID}=\frac{BA}{BD}=\frac{5}{2,5}=2\)
Do G là trọng tâm của tam giác ABC nên \(\frac{AG}{GT}=2\)
Từ các kết quả trên ta được \(\frac{AI}{ID}=\frac{AG}{GT}=2\)suy ra IG // DT hay IG // BC (Theo định lý Thales đảo)
b) Ta có \(\Delta BMI=\Delta BDI\)vì \(BD=BM=2,5;\widehat{DBI}=\widehat{MBI}\); BI là cạnh chung
Suy ra \(\widehat{BMI}=\widehat{BDI}\)
Chứng minh tương tự \(\Delta CNI=\Delta CDI\Rightarrow\widehat{ CNI}=\widehat{CDI}\)
Mà \(\widehat{BDI}+\widehat{CDI}=180^0\)nên \(\widehat{BMI}+\widehat{CNI}=180^0\)suy ra\(\widehat{AMI}+\widehat{ANI}=180^0\)
Vậy tứ giác AMIN nội tiếp hay bốn điểm A, M, I, N cùng nằm trên 1 đường tròn (đpcm)

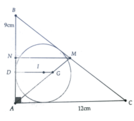
Gọi M là trung điểm của BC
Ta tính được AG = 2 3 AM = 10cm
Gọi N là trung điểm của AB => MN//AC, MN ⊥ AB
D,I,G thẳng hàng
<=> A G A M = A D A N = 2 3 <=> A D 2 A N = 1 3 <=> A D A B = 1 3
Ta có AD = r nội tiếp = A B + A C - B C 2 <=> A B 3 = A B + A C - B C 2
<=> AB+3AC = 3BC = A B 2 + A C 2
<=> 3AC = 4AB (đpcm)
Áp dụng kết quả trên ta có: AD = A B + A C - B C 2 = 3cm
=> ID = DA = 3cm => IG = DG – ID = 1cm