Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Xét (O) có
ΔBMC nội tiếp
BC là đường kính
Do đó: ΔBMC vuông tại M
Xét (O) có
ΔBNC nội tiếp
BC là đường kính
Do đo: ΔBNC vuông tại N
Xet ΔABC có
BN,CM là các đường cao
BN cắt CM tại H
Do đó; H là trực tâm
=>AH vuông góc với BC
a: Xét (O) có
ΔMBC nội tiếp
BC là đường kính
Do đó: ΔMBC vuông tại M
Xét (O) có
ΔNBC nội tiếp
BC là đường kính
Do đó:ΔNBC vuông tại N
Xét ΔABC có
BN là đường cao
CM là đường cao
BN cắt CM tại H
Do đó: AH⊥BC tại K
b: Xét ΔANB vuông tại N và ΔAMC vuông tại M có
\(\widehat{MAC}\) chung
Do đó: ΔANB∼ΔAMC
Suy ra: AN/AM=AB/AC
hay \(AN\cdot AC=AB\cdot AM\)
bài này trong đề thi có nè...mà mình hỏi ko ai biết làm,giáo viên cũng kêu khó
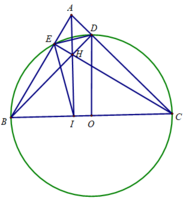
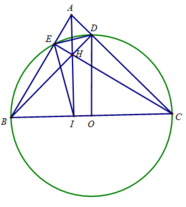
a ) Ta có : BC là đường kính của (O) \(\Rightarrow CM\perp AB,BN\perp AC\)
Mà \(BN\cap CM=H\Rightarrow H\) là trực tâm tam giác
\(\Rightarrow AK\perp BC\)
b ) Ta có : \(CM\perp AB,BN\perp AC\)
\(\Rightarrow\cos\widehat{A}=\frac{AM}{AC}=\frac{AN}{AB}\)
\(\Rightarrow AM.AB=AN.AC\)
c ) Ta có : \(AK\perp BC,BN\perp AC,CM\perp AB\)
\(\Rightarrow AMHN,MHKB,ANKB\) nội tiếp
\(\Rightarrow\widehat{KMH}=\widehat{KBH}=\widehat{KBN}=\widehat{KAN}=\widehat{HAN}=\widehat{HMN}\)
\(\Rightarrow MH\) là phân giác \(\widehat{NMK}\)
d ) Ta có :
\(\widehat{SMB}=\widehat{NCB}\left(+\widehat{BMN}=180^0\right)\)
\(\Rightarrow\Delta SMB\sim\Delta SCN\left(g.g\right)\Rightarrow\frac{SM}{SC}=\frac{SB}{SN}\Rightarrow SB.SC=SM.SN\)
Theo câu c ) \(\Rightarrow\widehat{NMK}=2\widehat{CMN}=2\widehat{NBC}=\widehat{NOC}\)
\(\Rightarrow MNOK\) nội tiếp
\(\Rightarrow\widehat{SKM}=\widehat{MNO}\)
\(\Rightarrow\Delta SMK\sim\Delta SON\left(g.g\right)\Rightarrow\frac{SM}{SO}=\frac{SK}{SN}\Rightarrow SM.SN=SK.SO\)
\(\Rightarrow SB.SC=SK.SO\)