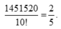Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Số cách xếp ngẫu nhiên là 10! cách.=
Ta tìm số cách xếp thoả mãn:
* Trước tiên xếp 2 học sinh lớp A có 2! cách.
Vì giữa hai học sinh lớp A không có học sinh lớp B nên chỉ có thể xếp học sinh lớp C vào giữa hai học sinh lớp A vừa xếp:
* Vậy chọn k ∈ 0 , 1 , 2 , 3 , 4 , 5 học sinh lớp C rồi xếp vào giữa hai học sinh lớp A có A 5 k cách, ta được một nhóm X.
* Xếp 10 - (2+k) = 8- k học sinh còn lại với nhóm X có (9 -k)! cách.
Vậy tất cả có ∑ 2 k = 0 5 ! A 5 k ( 9 - k ) ! = 1451520 cách xếp thỏa mãn
Xác suất cần tính bằng 1451520 10 ! = 2 5
Đáp án A
Kí hiệu học sinh các lớp 12A, 12B, 12C lần lượt là A, B, C
Ta sẽ xếp 5 học sinh của lớp 12C trước, khi đó xét các trường hợp sau:
TH1: CxCxCxCxCx với x thể hiện là ghế trống. Khi đó, số cách xếp là 
cách.
TH2: xCxCxCxCxC giống với TH1=> có 
cách xếp.
TH3: CxxCxCxCxC với xx là hai ghế trống liền nhau.
Chọn 1 học sinh lớp 12A và 1 học sinh lớp 12B vào hai ghế trống đó => 
cách xếp.
Ba ghế trống còn lại ta sẽ xếp 3 học sinh còn lại của 2 lớp 12A-12B => 
cách xếp.
Do đó, TH3 có 
cách xếp.
Ba TH4. CxCxxCxCxC.
TH5. CxCxCxxCxC.
TH6. CxCxCxCxCxx tương tự TH3.
Vậy có tất cả 
cách xếp cho các học sinh.
Suy ra xác suất cần tính là
Đáp án A
Kí hiệu học sinh các lớp 12A, 12B,12C lần lượt là A,B,C
Ta sẽ xếp 5 học sinh của lớp 12C trước, khi đó xét các trường hợp sau
Trường hợp1:
CxCxCxCxCx với x thể hiện là ghế trống.
Khi đó, số cách xếp là 5!5! cách.
Trường hợp 2: xCxCxCxCxC giống với TH1
⇒ có 5!5! cách xếp
Trường hợp 3: CxxCxCxCxC với xx là hai ghế trống liền nhau
Chọn 1 học sinh lớp 12A và 1 học sinh lớp 12B vào hai ghế trống đó
⇒ 2.3.2! cách xếp
Ba ghế trống còn lại ta sẽ xếp 3hoc sinh còn lại của 2 lớp 12A-12B
⇒ 3! cách xếp.
Do đó, TH3 có 2.3.2!.3!.5! cách xếp
Ba TH4. CxCxxCxCxC
TH5. CxCxCxxCxC
TH6. CxCxCxCxCxx tương tự
Vậy có tất cả 2.5!5!+4.2.3.2!.3!.5!=63360 cách xếp cho các học sinh
Suy ra xác suất cần tính là
P = 63360 10 ! = 11 630
Đáp án D
Coi 5 bạn của cả 12A và B vào một lớp 12X nào đó
Do số lượng ở đề nên ta có hai trường hợp
TH1. Các bạn 12C và 12X xen kẽ nhau.
Có 5 ! . 5 ! . 2 ! = 28800 cách
TH2. Có hai bạn lớp 12A và 12B dính với nhau
Ta có như 12X chỉ có 4 bạn. rồi lại làm xen kẽ
Chọn 2 bạn dính nhau và hoán vị 2 bạn đó có 12 cách, 5 bạn 12C tạo ra 4 khe để 4 bạn của lớp 12X đứng vào nên có tất cả là
12.5!.4!=34560
`n(\Omega)=6! =720`
`@TH1:` H/s lớp `C` ngồi đầu tiên hoặc cuối cùng.
`=>` Có `2.1.A_3 ^1 .4! =144` cách xếp h/s lớp `C` không ngồi cạnh lớp `B`.
`@TH2:` H/s lớp `C` không ngồi đầu cũng không ngồi cuối.
`=>` Có `4.A_3 ^2 .3! =144` cách xếp h/s lớp `C` không ngồi cạnh lớp `B`.
Gọi `A:`" H/s lớp `C` không ngồi cạnh h/s lớp `B`"
`=>n(A)=144.2=288`
`=>P(A)=288/720=2/5`
`->bb D`
TH1: 5 học sinh lớp C đứng cách nhau đúng 1 vị trí
- Chọn vị trí cho nhóm 5 học sinh lớp C: 2 cách (đứng đầu hàng hoặc ko đứng đầu hàng)
- Hoán vị 5 học sinh lớp C: 5! cách
- Hoán vị 5 học sinh lớp A và B: 5! cách
\(\Rightarrow2.5!.5!\) cách cho TH1
TH2: 5 học sinh lớp C trong đó có 2 bạn đứng cách nhau 2 vị trí
Chọn vị trí cho 2 người kề nhau: 4 cách
Hoán vị 5 học sinh lớp C: 5! cách
Chọn 1 học sinh lớp A, 1 học sinh lớp B xếp vào 2 vị trí liền kề nói trên: \(C_2^1.C_3^1.2!\) cách
Xếp vị trí cho 3 người còn lại: 3! cách
\(\Rightarrow4.5!.C_2^1.C_3^1.2!.3!\) cách cho TH2
Tổng cộng: \(TH1+TH2=...\)
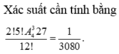
Chọn C
Số cách xếp ngẫu nhiên là 10! cách.
Ta tìm số cách xếp thoả mãn:
* Trước tiên xếp 2 học sinh lớp A có 2! cách.
Vì giữa hai học sinh lớp A không có học sinh lớp B nên chỉ có thể xếp học sinh lớp C vào giữa hai học sinh lớp A vừa xếp:
* Vậy chọn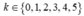
học sinh lớp C rồi xếp vào giữa hai học sinh lớp A có
A
5
k
cách, ta được một nhóm X.
* Xếp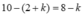
học sinh còn lại với nhóm X có (9-k)! cách.
Vậy tất cả có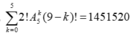
cách xếp thỏa mãn.
Xác suất cần tính bằng