Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Ba số: 2 x − 1 ; x ; 2 x + 1 theo thứ tự lập thành cấp số nhân
⇔ 2 x − 1 2 x + 1 = x 2 ⇔ 4 x 2 − 1 = x 2 ⇔ 3 x 2 = 1 ⇔ x = ± 1 3 .

Chọn B
Vì 2 x - 1 ; x ; 2 x + 1 theo thứ tự lập thành cấp số nhân nên
![]()
![]()

Chọn đáp án D
Phương pháp
Cho ba số a, b, c lập thành CSN thì ta có: b 2 = a c .
Cách giải
Ta có: ( x - 1 ) ( x - 3 ) ( x - m ) = 0
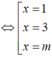
Phương trình đã cho có 3 nghiệm phân biệt
![]()
+) Giả sử 1; 3; m lập thành 1 CSN tăng
![]()
+) Giả sử m; 1; 3 lập thành 1 CSN tăng
![]()
+) Giả sử 1; m; 3 lập thành 1 CSN tăng
![]()
Vậy có 3 giá trị m thỏa mãn

Để 3 số hạng đó lập thành cấp số cộng, ta có :
\(\left(5^{1+x}+5^{1-x}\right)+\left(25^x+25^{-x}\right)=2\left(\frac{a}{2}\right)\)
\(\Leftrightarrow a=5\left(5^x+\frac{1}{5^x}\right)+\left(5^{2x}+\frac{1}{5^{2x}}\right)\)
Theo bất đẳng thức côsi, ta có : \(5^x+\frac{1}{5^x}\ge2\sqrt{1}=2,5^{2x}+\frac{1}{5^{2x}}\ge2\)
\(\Rightarrow a\ge5.2+2=12\)
Vậy với : \(a\ge12\), thì 3 số đó lập thành cấp số cộng.

1: Để ba số này lập thành 1 cấp số nhân thì
\(\left[{}\begin{matrix}\left(x+4\right)^2=\left(4x+8\right)\left(x+2\right)\\\left(x+2\right)^2=\left(x+4\right)\left(4x+8\right)\\\left(4x+8\right)^2=\left(x+2\right)\left(x+4\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(2x+4\right)^2-\left(x+4\right)^2=0\\4x^2+8x+16x+32-x^2-4x-4=0\\16x^2+64x+64-x^2-6x-8=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left(2x+4-x-4\right)\left(2x+4+x+4\right)=0\\3x^2+20x+28=0\\15x^2+58x+56=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x\left(3x+8\right)=0\\x\in\left\{-2;-\dfrac{14}{3}\right\}\\x\in\left\{-\dfrac{28}{15};-2\right\}\end{matrix}\right.\)
=>\(x\in\left\{0;-\dfrac{8}{3};-\dfrac{14}{3};-\dfrac{28}{15}\right\}\)
2:
Để đây là 1 cấp số nhân thì
\(\left[{}\begin{matrix}1^2=5\left(2x+4\right)\\5^2=1\cdot\left(2x+4\right)\\\left(2x+4\right)^2=1\cdot5\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}10x+20=1\\2x+4=25\\\left(2x+4\right)^2=5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{19}{10}\\x=\dfrac{21}{2}\\2x+4=\pm\sqrt{5}\end{matrix}\right.\)
=>\(x\in\left\{-\dfrac{19}{10};\dfrac{21}{2};\dfrac{\sqrt{5}-4}{2};\dfrac{-\sqrt{5}-4}{2}\right\}\)

1, Ta có \(\left(x+4\right)^2=\left(x+2\right)\left(4x+8\right)\Leftrightarrow x^2+8x+16=4x^2+12x+16\)
\(\Leftrightarrow3x^2+4x=0\Leftrightarrow x\left(3x+4\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{4}{3}\end{matrix}\right.\)
2, tương tự

\(2x - 1;x;2x + 1\) theo thứ tự lập thành cấp số nhân khi:
\({x^2} = \left( {2x - 1} \right)\left( {2x + 1} \right) \Leftrightarrow {x^2} = 4{{\rm{x}}^2} - 1 \Leftrightarrow 3{{\rm{x}}^2} - 1 = 0 \Leftrightarrow x = \pm \frac{{\sqrt 3 }}{3}\)
Vậy có 2 số thực \(x\) thoả mãn \(2x - 1;x;2x + 1\) theo thứ tự lập thành cấp số nhân.
Chọn B.
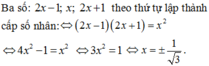
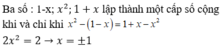
Đáp án A