SL
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PK
2
MH
1
9 tháng 7 2018
Nếu đề bài là giải phương trình thì :
\(\sqrt{x+3}=\sqrt{x-3}\)
Đk : \(x\ge3\)
Bình phương hai vế :
\(\Rightarrow x+3=x-3\)
\(x+3-x+3=0\)
\(0x=-6\)
\(\Rightarrow\)phương trình vô nghiệm
AP
1
DH
1
24 tháng 9 2021
\(\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{AC}{BC}:\dfrac{AB}{BC}=\dfrac{AC}{AB}=\tan\alpha\)
\(\dfrac{\cos\alpha}{\sin\alpha}=\dfrac{AB}{BC}:\dfrac{AC}{BC}=\dfrac{AB}{AC}=\cot\alpha\)
\(\tan\alpha\cot\alpha=\dfrac{AC}{AB}\cdot\dfrac{AB}{AC}=1\)
\(\sin^2\alpha+\cos^2\alpha=\dfrac{AC^2}{BC^2}+\dfrac{AB^2}{BC^2}=\dfrac{AB^2+AC^2}{BC^2}=\dfrac{BC^2}{BC^2}=1\left(pytago\right)\)
25 tháng 5 2021
`A=1/(x+sqrtx)+(2sqrtx)/(x-1)-1/(x-sqrtx)`
`=(sqrtx-1+2x-sqrtx-1)/(sqrtx(x-1))`
`=(2x-2)/(sqrtx(x-1))`
`=2/sqrtx`
`b)A=1`
`<=>2/sqrtx=1`
`<=>sqrtx=2`
`<=>x=4(tm)`
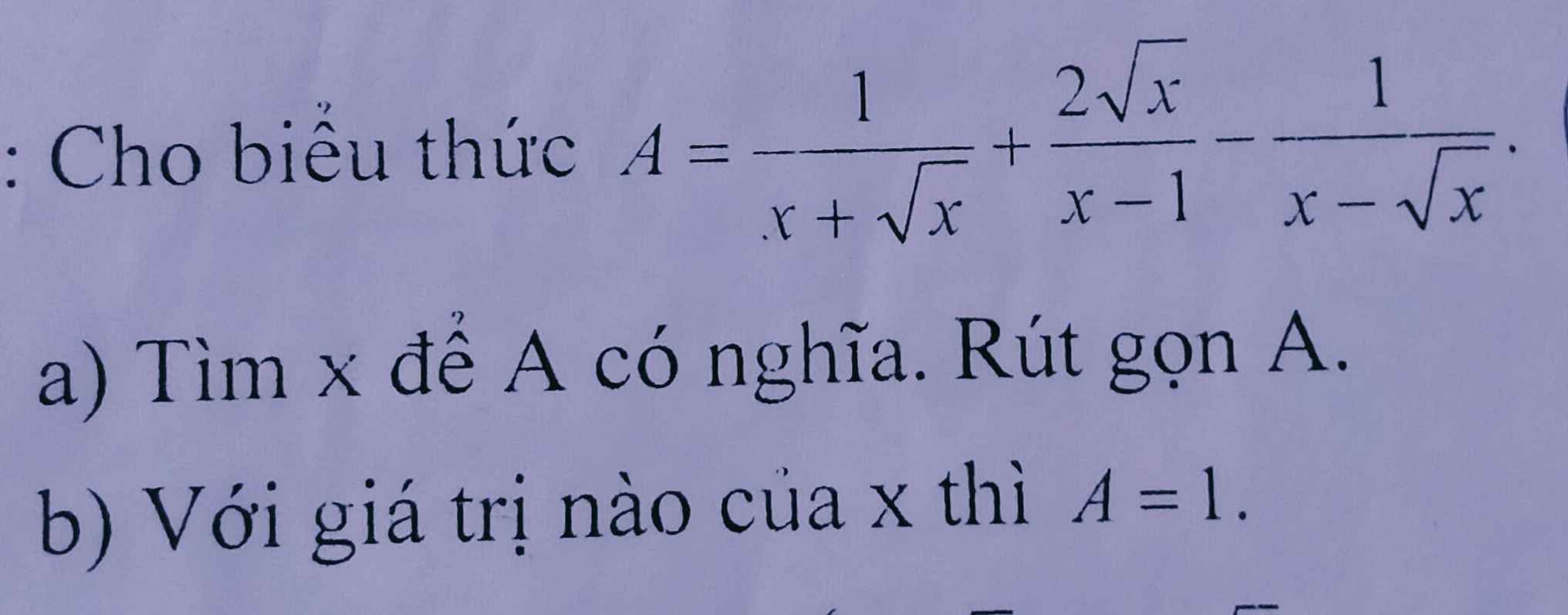
Giải giúp e vs ạ ,e đang cần gấp
ĐK: \(x>0\)
PT trở thành:
\(x+2=3\sqrt{x}\\ \Leftrightarrow x-3\sqrt{x}+2=0\\ \Leftrightarrow x-2\sqrt{x}-\sqrt{x}+2=0\\ \Leftrightarrow\sqrt{x}\left(\sqrt{x}-2\right)-\left(\sqrt{x}-2\right)=0\\ \Leftrightarrow\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x}-2=0\\\sqrt{x}-1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\x=1\left(tm\right)\end{matrix}\right.\)
Vậy PT có nghiệm `x=4` hoặc `x=1`
\(\dfrac{x+2}{\sqrt{x}}=3\) (ĐKXĐ: x > 0)
\(\Leftrightarrow x+2=3\sqrt{x}\)
\(\Leftrightarrow x-3\sqrt{x} +2=0\)
\(\Leftrightarrow x-\sqrt{x}-2\sqrt{x}+2=0\)
\(\Leftrightarrow\sqrt{x}\left(\sqrt{x}-1\right)-2\left(\sqrt{x}-1\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}-2=0\\\sqrt{x}-1=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=1\end{matrix}\right.\) (tm)
#Ayumu