Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: A là tập nghiệm của đa thức P(x)
\( \Rightarrow A = \{ x \in \mathbb{R}|P(x) = 0\} \)
Để biểu thức \(\dfrac{1}{{P(x)}}\) xác định thì \(P(x) \ne 0\) hay \(x \notin A\).
Gọi B là tập hợp các số thực x sao cho biểu thức \(\dfrac{1}{{P(x)}}\) xác định.
\( \Rightarrow B =\{ x \in \mathbb{R}|P(x) \ne 0\}= \left\{ {x \in \mathbb{R}|x \notin A} \right\} = \mathbb{R}\,{\rm{\backslash }}\,A\)

Bước 1:
Số tiền bán x vé loại 1 là: \(x.50\) (nghìn đồng)
Số tiền bán y vé loại 2 là: \(y.100\) (nghìn đồng)
Bước 2:
Số tiền thu được là
\(50x + 100y\) (nghìn đồng)
a)
Ta có 20 triệu = 20 000 (nghìn đồng)
Số tiền thu được khi bán x vé loại 1 và y vé loại 2 là \(50x + 100y\) (nghìn đồng)
Nên để số tiền thu được tối thiểu 20 triệu thì ta cần:
\(\begin{array}{l}50x + 100y \ge {20 000}\\ \Leftrightarrow x + 2y \ge 400\end{array}\)
Vậy các số nguyên không âm x và y phải thỏa mãn điều kiện \(x + 2y \ge 400\)
b)
Số tiền thu được khi bán x vé loại 1 và y vé loại 2 là \(50x + 100y\) (nghìn đồng)
Số tiền thu được nhỏ hơn 20 triệu thì:
\(\begin{array}{l}50x + 100y < {20 000}\\ \Leftrightarrow x + 2y < 400\end{array}\)
Chú ý:
- Số tiền tối thiểu thì ta phải lập bất phương trình với dấu “\( \ge \)”.
- Cần đổi 20 triệu đồng thành 20 000 nghìn đồng tránh lập sai bất phương trình.

a, Biểu thức đại số biểu thị số tiền Hà phải trả là:
\(5000.2+4000x=10000+4000x\)
b, Biểu thức số tiền Huy phải trả là :
\(4000.\left(x+3\right)=4000x+12000\)
a) Biểu thức đại số số tiền Hà phải trả là : \(5000.2+4000.x\)(đồng)
b) Biểu thức đại số số tiền Huy phải trả là: \(\left(x+3\right).4000=4000x+12000\) (đồng)

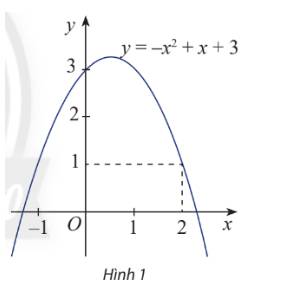
a) Số mũ cao nhất của hàm số là 2, suy ra biểu thức\(f\left( x \right)\)đã cho là đa thức bậc hai
b) Thay \(x = 2\) vào \(f\left( x \right)\) ta có:
\(f\left( 2 \right) = - {2^2} + 2 + 3 = 1 > 0\)
Suy ra \(f\left( 2 \right)\) dương.
a) xy
b)x+y +5xy